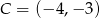Zadanie nr 4626381
Punkty 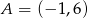 i
i 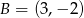 są wierzchołkami trójkąta
są wierzchołkami trójkąta 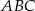 . Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne
. Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne 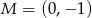 oblicz współrzędne wierzchołka
oblicz współrzędne wierzchołka 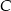 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
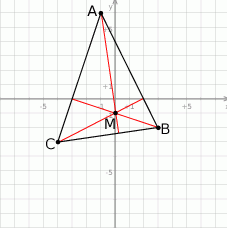
Jak wyliczyć współrzędne wierzchołka 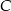 ? Widać, że w miarę łatwo można napisać równanie wysokości
? Widać, że w miarę łatwo można napisać równanie wysokości 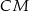 : jest prostopadła do
: jest prostopadła do 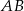 i przechodzi przez
i przechodzi przez 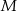 . Podobnie, możemy napisać równanie jednego z boków, powiedzmy
. Podobnie, możemy napisać równanie jednego z boków, powiedzmy 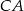 : jest on prostopadły do
: jest on prostopadły do 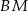 i przechodzi przez
i przechodzi przez 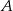 . Punkt wspólny tych dwóch prostych to punkt
. Punkt wspólny tych dwóch prostych to punkt 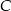 .
.
Sposób I
Zadanie jest dość proste jeżeli skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p ,q]](https://img.zadania.info/zad/4626381/HzadR9x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 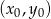 :
:
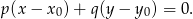
Najpierw piszemy równanie wysokości 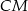 : mamy
: mamy ![→ →v = AB = [4,− 8]](https://img.zadania.info/zad/4626381/HzadR13x.gif) i punkt
i punkt 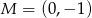 .
.
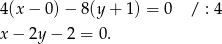
Teraz piszemy równanie prostej 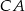 : mamy
: mamy ![→ → v = BM = [− 3,1]](https://img.zadania.info/zad/4626381/HzadR17x.gif) i punkt
i punkt 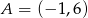 .
.
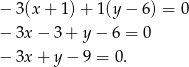
Szukamy teraz punktu wspólnego otrzymanych prostych, czyli rozwiązujemy układ równań
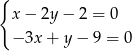
Dodając do drugiego równania 3 razy pierwsze (żeby skrócić  ) mamy
) mamy 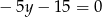 , czyli
, czyli 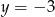 . Z pierwszego równania mamy
. Z pierwszego równania mamy 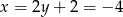 . Zatem
. Zatem 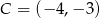 .
.
Sposób II
Jeżeli nie chcemy używać wzoru na równanie prostej prostopadłej do wektora i przechodzącej przez punkt, to musimy się odrobinę bardziej namęczyć. Zacznijmy od napisania prostej 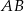 . Można to zrobić ze wzoru na równanie prostej przez dwa punkty, ale my będziemy wszystko robić wprost. Szukamy prostej
. Można to zrobić ze wzoru na równanie prostej przez dwa punkty, ale my będziemy wszystko robić wprost. Szukamy prostej 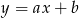 spełniającej
spełniającej
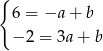
Odejmując od drugiego równania pierwsze mamy 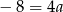 , czyli
, czyli 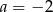 . I tak naprawdę to nam wystarczy, bo jest nam potrzebny tylko kierunek prostej
. I tak naprawdę to nam wystarczy, bo jest nam potrzebny tylko kierunek prostej 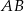 , współczynnik
, współczynnik 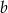 nie ma znaczenia.
nie ma znaczenia.
Szukamy teraz prostej 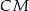 , czyli prostej prostopadłej do
, czyli prostej prostopadłej do 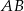 i przechodzącej przez
i przechodzącej przez 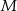 . Jest ona postaci
. Jest ona postaci 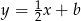 (bo jest prostopadła do
(bo jest prostopadła do 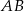 ). Współczynnik
). Współczynnik 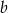 wyznaczamy wstawiając punkt
wyznaczamy wstawiając punkt 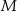 .
.
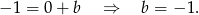
Zatem 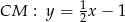 .
.
Teraz zajmijmy się prostą 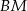 . Szukamy
. Szukamy 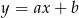 tak, aby
tak, aby
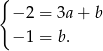
Wstawiając 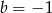 do pierwszego równania mamy
do pierwszego równania mamy
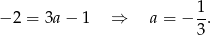
Zatem prosta 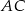 będzie miała współczynnik 3, czyli będzie postaci
będzie miała współczynnik 3, czyli będzie postaci 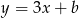 . Współczynnik
. Współczynnik 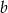 wyznaczamy wstawiając punkt
wyznaczamy wstawiając punkt 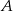 .
.

Pozostało znaleźć punkt wspólny prostych 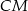 i
i 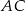 .
.
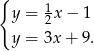
Porównując 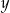 -ki mamy
-ki mamy
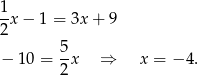
Wtedy 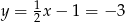 .
.
Odpowiedź: