Zadanie nr 4683773
Punkty 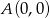 oraz
oraz 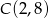 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 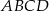 o boku długości
o boku długości 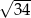 . Wyznacz współrzędne pozostałych wierzchołków tego rombu.
. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Rozwiązanie
Jak zawsze zaczynamy od schematycznego rysunku.
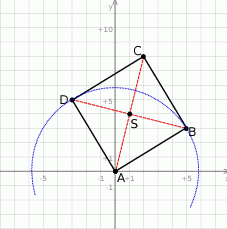
Sposób I
Aby wyznaczyć pozostałe wierzchołki, wystarczy znaleźć punkty, które są odległe od 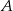 i
i 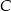 o
o 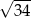 . W tym celu wystarczy znaleźć punkty wspólne okręgów o środkach w punktach
. W tym celu wystarczy znaleźć punkty wspólne okręgów o środkach w punktach 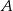 i
i 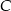 i promieniu
i promieniu 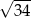 . W ten sposób dostajemy układ równań
. W ten sposób dostajemy układ równań
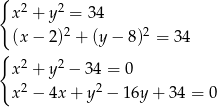
Odejmując od pierwszego równania drugie (żeby skrócić kwadraty) mamy
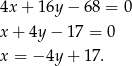
Wyliczoną wartość  podstawiamy do równania pierwszego okręgu i mamy
podstawiamy do równania pierwszego okręgu i mamy
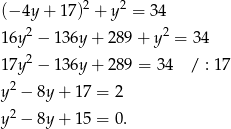
Liczymy, 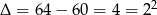 , co daje
, co daje
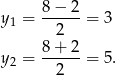
Mamy stąd 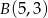 oraz
oraz 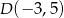 .
.
Sposób II
Co możemy wyliczyć mając dwa przeciwległe wierzchołki rombu? – możemy wyliczyć środek 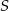 łączącego je odcinka. Ponieważ przekątne rombu dzielą się na połowy,
łączącego je odcinka. Ponieważ przekątne rombu dzielą się na połowy, 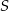 to dokładnie punkt przecięcia się przekątnych. Ponadto przekątne rombu są prostopadłe, co pozwoli nam napisać równanie drugiej przekątnej. Jak już będziemy mieli to równanie, to sprawa będzie prosta – znajdziemy na niej punkty odległe od
to dokładnie punkt przecięcia się przekątnych. Ponadto przekątne rombu są prostopadłe, co pozwoli nam napisać równanie drugiej przekątnej. Jak już będziemy mieli to równanie, to sprawa będzie prosta – znajdziemy na niej punkty odległe od 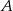 o
o 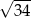 . Mamy plan działania, zatem do dzieła.
. Mamy plan działania, zatem do dzieła.
Środek 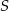 odcinka
odcinka 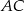 :
:
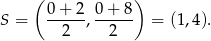
Aby napisać równanie drugiej przekątnej skorzystamy ze wzoru na prostą prostopadłą do wektora ![→ v = [v1,v2]](https://img.zadania.info/zad/4683773/HzadR22x.gif) i przechodzącą przez punkt
i przechodzącą przez punkt 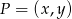 :
:
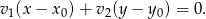
W naszej sytuacji
![→ → v = AC = [2,8],](https://img.zadania.info/zad/4683773/HzadR25x.gif)
co daje nam równanie prostej 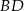
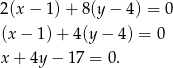
Pozostało znaleźć na tej prostej punkty w odległości 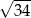 od
od 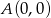 . W tym celu szukamy punktów wspólnych tej prostej z okręgiem
. W tym celu szukamy punktów wspólnych tej prostej z okręgiem 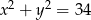 .
.
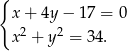
Z pierwszego równania wyliczamy 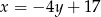 i wstawiamy do drugiego równania. Dalsze rachunki są identyczne jak w pierwszym sposobie.
i wstawiamy do drugiego równania. Dalsze rachunki są identyczne jak w pierwszym sposobie.
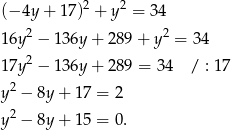
Liczymy 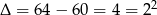 , co daje
, co daje
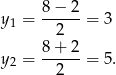
Mamy stąd 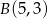 oraz
oraz 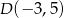 .
.
Odpowiedź: 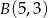 ,
,