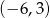Zadanie nr 4709074

Wyznacz środek okręgu wpisanego w trójkąt, którego boki zwierają się w prostych o równaniach 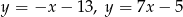y = −x − 13 , y = 7x− 5 oraz y = x + 19 .

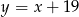Rozwiązanie

Rozpoczynamy od naszkicowania opisanej sytuacji.

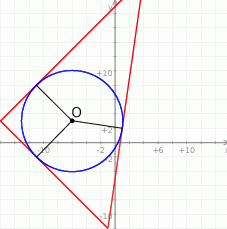
Szukamy punktu 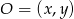O = (x,y) , który jest równoodległy od trzech podanych prostych. To, że jest równoodległy od pierwszych dwóch możemy zapisać w postaci

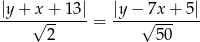
|y-+-x-+-13| |y−-7x-+--5| √ -- = √ --- 2 50

Aby opuścić wartości bezwzględne musimy zauważyć, że punkt 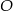leży powyżej każdej z nich, czyli mamy równanie

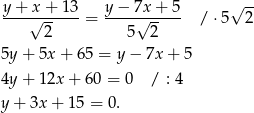
y + x + 13 y − 7x + 5 √ -- ----√------= ----√------ / ⋅5 2 2 5 2 5y + 5x + 65 = y− 7x+ 5 4y + 12x + 60 = 0 / : 4 y+ 3x + 15 = 0 .

Potrzebujemy jeszcze jedno równanie – zapiszmy, że punkt 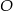jest równoodległy od pierwszej i trzeciej prostej.

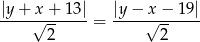
|y + x + 13| |y− x − 19| -----√------ = ----√------- 2 2

Punkt 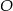leży powyżej pierwszej z nich i poniżej drugiej, czyli

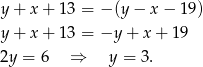
y + x + 13 = − (y− x− 19) y + x + 13 = −y + x+ 19 2y = 6 ⇒ y = 3.

Zatem z poprzedniego równania mamy

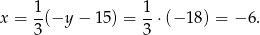
1 1 x = -(−y − 15) = --⋅(− 18) = − 6. 3 3

Mamy więc 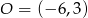O = (− 6,3) .
Odpowiedź: