Zadanie nr 4777413
Punkty 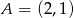 i
i 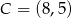 są przeciwległymi wierzchołkami prostokąta, którego bok
są przeciwległymi wierzchołkami prostokąta, którego bok 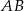 jest równoległy do osi
jest równoległy do osi 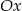 . Punkty
. Punkty 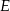 i
i 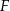 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 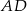 i
i 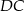 . Oblicz pole trójkąta
. Oblicz pole trójkąta 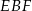 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
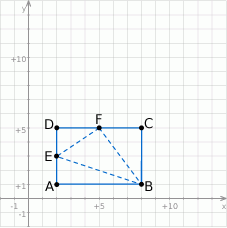
Skoro boki prostokąta są równoległe do osi układu, to pozostałe wierzchołki mają współrzędne
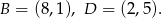
Pole trójkąta 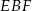 możemy obliczyć odejmując od pola prostokąta
możemy obliczyć odejmując od pola prostokąta 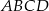 pola trójkątów prostokątnych
pola trójkątów prostokątnych 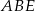 ,
, 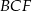 i
i 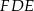 .
.
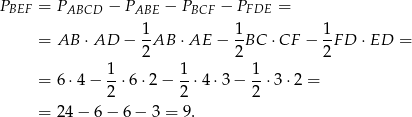
Odpowiedź: 9

