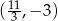Zadanie nr 4784338
Znajdź punkt dzielący wektor 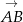 o końcach
o końcach 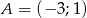 ,
, 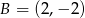 w stosunku -4.
w stosunku -4.
Rozwiązanie
Szukamy punktu 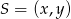 o własności
o własności
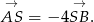
Mamy więc równanie
![[x + 3,y − 1] = − 4[2− x,− 2− y] [x + 3,y − 1] = [− 8+ 4x,8 + 4y].](https://img.zadania.info/zad/4784338/HzadR2x.gif)
Mamy stąd równania
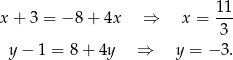
Odpowiedź: 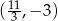
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Znajdź punkt dzielący wektor 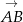 o końcach
o końcach 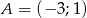 ,
, 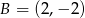 w stosunku -4.
w stosunku -4.
Szukamy punktu 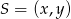 o własności
o własności
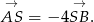
Mamy więc równanie
![[x + 3,y − 1] = − 4[2− x,− 2− y] [x + 3,y − 1] = [− 8+ 4x,8 + 4y].](https://img.zadania.info/zad/4784338/HzadR2x.gif)
Mamy stąd równania
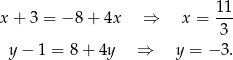
Odpowiedź: