Zadanie nr 4852794
W trójkącie 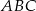 dane są:
dane są: 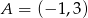 ,
, ![→ AB = [5,− 4]](https://img.zadania.info/zad/4852794/HzadT2x.gif) oraz
oraz ![→ BC = [2,6]](https://img.zadania.info/zad/4852794/HzadT3x.gif) . Trójkąt
. Trójkąt 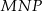 jest obrazem trójkąta
jest obrazem trójkąta 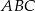 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 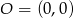 i skali
i skali 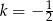 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 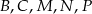 .
.
Rozwiązanie
Warto zacząć od schematycznego rysunku.
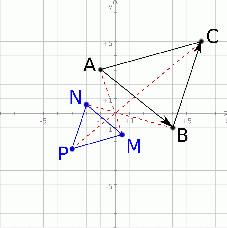
Widać, że łatwo możemy wyliczyć współrzędne punktów 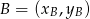 i
i 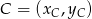 .
.
![→ [5,− 4] = AB = [x + 1,y − 3] ⇒ B = (4,− 1) → B B [2,6] = BC = [x − 4 ,y + 1] ⇒ C = (6,5). C C](https://img.zadania.info/zad/4852794/HzadR3x.gif)
Z podanej informacji o jednokładności wiemy, że
![( ) → 1 → 1 1 3 [xM ,yM ] = OM = − -OA = − -[− 1,3] ⇒ M = -,− -- 2 2 ( 2 2) → 1-→ 1- 1- [xN ,yN ] = ON = − 2OB = − 2[4,− 1] ⇒ N = − 2,2 → → ( ) [x ,y ] = OP = − 1OC = − 1[6,5] ⇒ P = − 3,− 5- . P P 2 2 2](https://img.zadania.info/zad/4852794/HzadR4x.gif)
Odpowiedź: 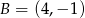 ,
, 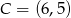 ,
, 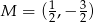 ,
, 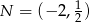 ,
,