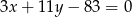/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4915456

Dodaj do ulubionych
Dodaj do rozwiązanych

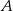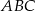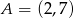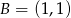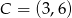Napisz równanie prostopadłej opuszczonej z wierzchołka A trójkąta ABC o wierzchołkach A = (2,7) , B = (1,1) i C = (3,6) na środkową 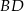BD boku AC .

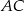Rozwiązanie

Zacznijmy od schematycznego rysunku.

PIC

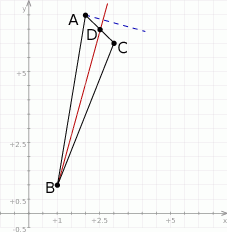
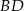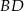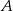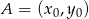
Narzucający się plan jest następujący. Piszemy równanie środkowej BD i znajdujemy równanie prostej prostopadłej do BD , przechodzącej przez punkt A . My zrobimy to jednak odrobinę prościej, korzystając ze wzoru na prostą prostopadłą do wektora → v = [a,b] i przechodzącą przez punkt A = (x0,y 0)

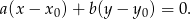
a(x − x0) + b(y − y0) = 0 .

W naszej sytuacji mamy 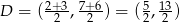D = (2+3, 7+-6) = (5, 13) 2 2 2 2 i → →v = BD = [3, 11] 2 2 . Zatem szukane równanie to

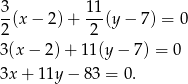
3 11 2-(x− 2)+ 2-(y − 7 ) = 0 3(x − 2) + 11(y − 7 ) = 0 3x + 11y − 83 = 0.

 
Odpowiedź: 3x + 11y − 83 = 0

Wersja PDF