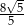/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4940047

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz odległość środka okręgu 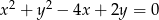2 2 x + y − 4x + 2y = 0 od prostej y = 2x + 3 .

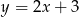Rozwiązanie

Przekształćmy równanie danego okręgu tak, aby było widać jaki jest jego środek i promień.

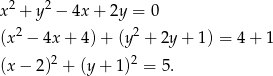
2 2 x + y − 4x + 2y = 0 (x2 − 4x + 4 )+ (y2 + 2y + 1 ) = 4+ 1 (x − 2)2 + (y + 1)2 = 5.

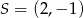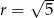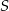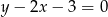Jest to więc okrąg o środku S = (2 ,−1 ) i promieniu √ -- r = 5 . Liczymy odległość punku S od danej prostej y− 2x − 3 = 0 .

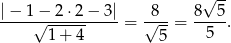
√ -- |− 1− 2⋅2 − 3 | 8 8 5 -----√-----------= √---= ----. 1+ 4 5 5

 
Odpowiedź: √ - 8-55

Wersja PDF