/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4947979

Dodaj do ulubionych
Dodaj do rozwiązanych

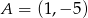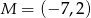Dane są punkty A = (1,− 5) i M = (− 7,2 ) oraz prosta 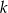k o równaniu 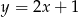y = 2x+ 1 . Wierzchołek 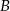B trójkąta 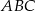ABC to punkt przecięcia prostej 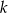k z prostą 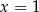x = 1 , a wierzchołek 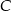C jest punktem przecięcia prostej 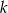k z prostą 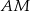AM . Oblicz pole trójkąta ABC .

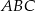Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

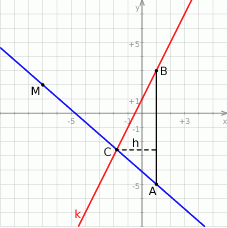
Wyznaczmy najpierw punkt 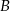B przecięcia prostej 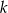k z prostą 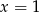x = 1 (podstawiamy 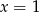x = 1 w równaniu tej prostej).

y = 2 + 1 = 3 .

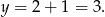
W takim razie 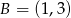B = (1,3 ) .

Piszemy teraz równanie prostej 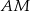AM – szukamy prostej w postaci 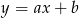y = ax+ b i podstawiamy współrzędne punktów 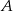A i M .

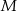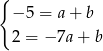
{ − 5 = a+ b 2 = − 7a + b

Odejmujemy od pierwszego równania drugie (żeby skrócić 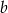b ) i mamy 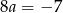8a = − 7 , czyli 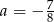7 a = − 8 . Z pierwszego równania wyznaczamy b .

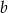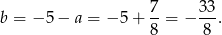
7 33 b = − 5 − a = − 5 + --= − ---. 8 8

Prosta 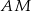AM ma więc równanie 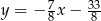y = − 7x − 33 8 8 . Szukamy teraz punktu wspólnego 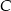C tej prostej z prostą k .

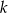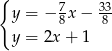
{ 7 33 y = − 8 x− 8 y = 2x + 1

Odejmujemy od drugiego równania pierwsze (żeby skrócić 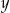y ) i mamy

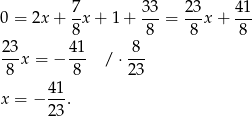
7 33 23 41 0 = 2x + 8-x+ 1+ -8-= -8 x + 8-- 23x = − 41- / ⋅-8- 8 8 23 41- x = − 23 .

Stąd

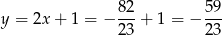
y = 2x + 1 = − 82-+ 1 = − 59- 23 23

i 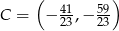( ) C = − 4213,− 5293 . Pole trójkąta 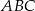ABC jest więc równe

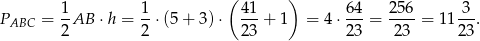
( ) P = 1AB ⋅h = 1⋅(5 + 3 )⋅ 41-+ 1 = 4 ⋅ 6-4 = 2-56 = 11 3-. ABC 2 2 23 2 3 23 23

 
Odpowiedź: 256 3 -23 = 11 23

Wersja PDF