/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 5041341

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wartość parametru 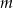m , dla której odległość punktu 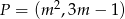2 P = (m ,3m − 1) od prostej 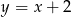y = x + 2 jest najmniejsza możliwa.

Rozwiązanie

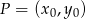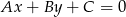Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

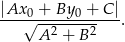
|Ax-0√-+-By-0 +-C|. A 2 + B 2

Mamy zatem

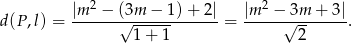
|m-2-−-(3m-−--1)+--2| |m-2 −-3m-+-3| d(P ,l) = √ 1 + 1 = √ 2 .

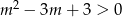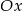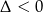Zauważmy teraz, że m 2 − 3m + 3 > 0 , bo wykresem lewej strony jest parabola, która w całości znajduje się powyżej osi Ox (bo Δ < 0 ). Mamy zatem

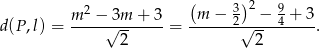
( 3)2 9 m-2 −-3m-+-3- -m-−--2--−--4-+-3- d(P ,l) = √ 2- = √ 2- .

Widać teraz, że odległość punktu 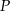P od danej prostej jest najmniejsza dla 3 m = 2 .  
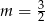Odpowiedź: m = 32

Wersja PDF