Zadanie nr 5094905
Boki 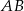 i
i 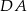 równoległoboku
równoległoboku 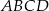 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 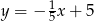 i
i 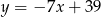 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 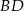 tego równoległoboku, jeżeli jego środek ma współrzędne
tego równoległoboku, jeżeli jego środek ma współrzędne 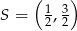 .
.
Rozwiązanie
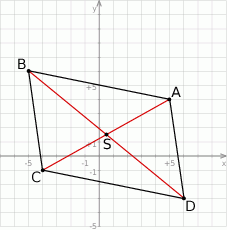
Szkicujemy równoległobok z przekątnymi (nasz rysunek jest dość dokładny, ale do rozwiązania wystarczy zwykły schematyczny szkic równoległoboku – nie musi być nawet w układzie współrzędnych).
Rozpoczynamy od wyznaczenia punktu 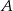 – jest to punkt wspólny dwóch podanych prostych.
– jest to punkt wspólny dwóch podanych prostych.
Porównujemy  -ki i mamy
-ki i mamy
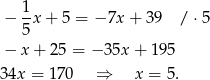
Stąd 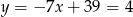 i
i 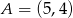 .
.
Teraz wyznaczymy współrzędne wierzchołka 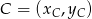 – punkt
– punkt 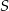 jest środkiem odcinka
jest środkiem odcinka 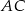 , więc
, więc
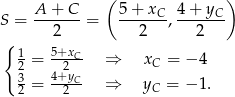
Zatem 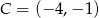 . Aby wyznaczyć współrzędne punktu
. Aby wyznaczyć współrzędne punktu 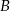 piszemy równanie prostej
piszemy równanie prostej 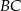 . Prosta ta jest równoległa do
. Prosta ta jest równoległa do 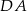 , więc ma równanie postaci
, więc ma równanie postaci 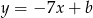 . Współczynnik
. Współczynnik 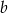 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 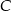 .
.
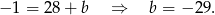
Prosta 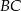 ma więc równanie
ma więc równanie 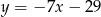 . Wyznaczamy teraz jej punkt wspólny
. Wyznaczamy teraz jej punkt wspólny 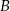 z prostą
z prostą 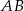 .
.
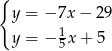
Porównujemy 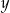 -ki i mamy
-ki i mamy
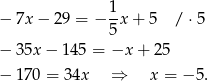
Stąd 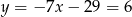 i
i 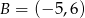 . Pozostało teraz napisać równanie prostej
. Pozostało teraz napisać równanie prostej 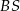 (czyli przekątnej
(czyli przekątnej 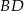 ). Szukamy prostej w postaci
). Szukamy prostej w postaci 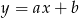 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 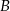 i
i 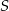 .
.
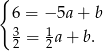
Odejmujemy od drugiego równania pierwsze i mamy
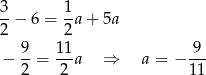
Stąd
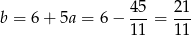
i przekątna 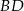 ma równanie
ma równanie 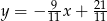 .
.
Odpowiedź: