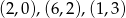/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 5318382

Dodaj do ulubionych
Dodaj do rozwiązanych

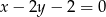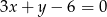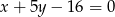Wyznacz współrzędne wierzchołków trójkąta, którego boki zawarte są w prostych o równaniach x − 2y − 2 = 0 , 3x + y − 6 = 0 , x + 5y − 16 = 0 .

Rozwiązanie

Szukane punkty, to punkty wspólne podanych prostych. Znajdźmy najpierw punkt wspólny pierwszych dwóch, czyli rozwiążmy układ równań

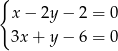
{ x− 2y− 2 = 0 3x+ y− 6 = 0

Dodając do pierwszego równania 2 razy drugie (żeby skrócić 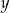y ) mamy

7x − 14 = 0 ⇒ x = 2.

Zatem z drugiego równania mamy

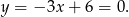
y = −3x + 6 = 0.

Oznaczmy sobie ten pierwszy wierzchołek trójkąta przez 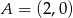A = (2,0) .

Szukamy teraz punktu wspólnego pierwszej i trzeciej prostej.

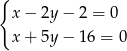
{ x − 2y − 2 = 0 x + 5y − 16 = 0

Odejmujemy od drugiego równania pierwsze (żeby skrócić x ) i mamy

7y − 14 = 0 ⇒ y = 2.

Za pierwszego równania mamy

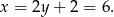
x = 2y+ 2 = 6.

Oznaczmy ten punkt przez B = (6,2) .

Pozostało znaleźć punkt wspólny drugiej i trzeciej prostej.

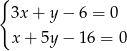
{ 3x + y − 6 = 0 x + 5y − 16 = 0

Odejmujemy od pierwszego równania 3 razy drugie (żeby skrócić x ) i mamy

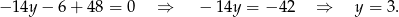
−1 4y− 6+ 48 = 0 ⇒ − 14y = − 42 ⇒ y = 3.

Z drugiego równania mamy

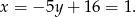
x = − 5y + 16 = 1.

Zatem trzeci wierzchołek to 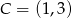C = (1,3 ) .

Na koniec możemy sobie narysować całą sytuację.

PIC

 
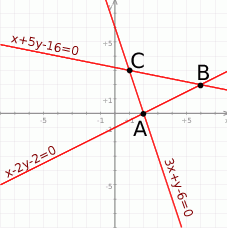
Odpowiedź: (2,0),(6,2),(1 ,3 )

Wersja PDF