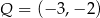/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 5321445

Dodaj do ulubionych
Dodaj do rozwiązanych

Prosta o równaniu 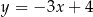y = − 3x + 4 jest symetralną odcinka 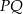P Q , gdzie 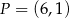P = (6,1) . Oblicz współrzędne punktu Q .

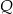Rozwiązanie

Symetralna odcinka jest do niego prostopadła, więc prosta 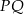PQ ma równanie postaci

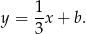
y = 1x + b. 3

Współczynnik 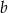b wyznaczamy podstawiając współrzędne punktu P .

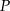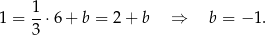
1 1 = --⋅6 + b = 2 + b ⇒ b = − 1. 3

Środek 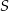S odcinka 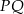P Q to punkt wspólny prostej 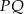PQ i podanej symetralnej.

PIC

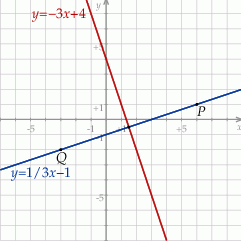
Wyznaczmy jego współrzędne.

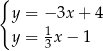
{ y = − 3x+ 4 y = 1x − 1 3

Odejmujemy od drugiego równania pierwsze i mamy

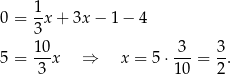
1 0 = -x + 3x − 1 − 4 3 5 = 10x ⇒ x = 5 ⋅-3-= 3. 3 10 2

Stąd

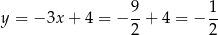
y = − 3x + 4 = − 9-+ 4 = − 1- 2 2

i 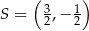(3 1) S = 2,− 2 .

Pozostało skorzystać ze wzoru na środek odcinka.

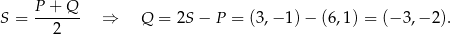
S = P-+-Q-- ⇒ Q = 2S − P = (3,− 1) − (6,1) = (− 3,− 2). 2

 
Odpowiedź: Q = (− 3,− 2)

Wersja PDF