Zadanie nr 5425996
Punkty 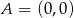 i
i 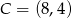 są wierzchołkami rombu
są wierzchołkami rombu 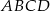 , którego jeden z boków zawiera się w prostej
, którego jeden z boków zawiera się w prostej 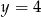 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
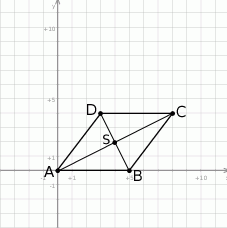
Widać, że boki 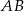 i
i 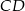 mają równania odpowiednio
mają równania odpowiednio 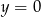 i
i 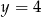 (druga prosta jest podana w treści, a pierwsza musi być do niej równoległa i musi przechodzić przez
(druga prosta jest podana w treści, a pierwsza musi być do niej równoległa i musi przechodzić przez 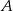 , więc jest to
, więc jest to 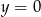 ). Pozostałe dwa wierzchołki wyznaczymy pisząc równanie przekątnej
). Pozostałe dwa wierzchołki wyznaczymy pisząc równanie przekątnej 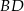 i znajdując jej punkty wspólne z prostymi
i znajdując jej punkty wspólne z prostymi 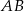 i
i 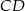 .
.
Środek 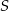 przekątnej
przekątnej 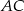 ma współrzędne
ma współrzędne
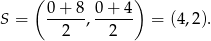
Prosta 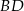 jest prostopadła do prostej
jest prostopadła do prostej 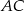 i przechodzi przez
i przechodzi przez 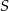 . Wyznaczymy jej równanie na dwa sposoby.
. Wyznaczymy jej równanie na dwa sposoby.
Sposób I
Napiszmy najpierw równanie prostej 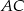 . Skoro przechodzi ona przez punkt
. Skoro przechodzi ona przez punkt 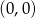 to jest postaci
to jest postaci 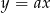 . Podstawiając w tym równaniu współrzędne punktu
. Podstawiając w tym równaniu współrzędne punktu 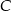 mamy
mamy
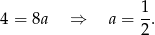
Zatem prosta 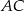 ma równanie
ma równanie 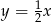 , a prosta
, a prosta 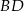 jako prostopadła do niej ma postać
jako prostopadła do niej ma postać 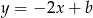 . Współczynnik
. Współczynnik 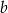 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 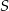 .
.

Zatem równanie 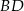 to
to  . Znajdźmy jej punkt wspólny z prostą
. Znajdźmy jej punkt wspólny z prostą 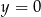 :
:
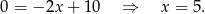
Zatem 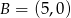 . Teraz znajdujemy punkt wspólny z prostą
. Teraz znajdujemy punkt wspólny z prostą 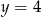 .
.
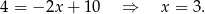
Zatem 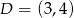 .
.
Sposób II
Równanie prostej 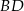 można bardzo szybko napisać korzystając ze wzoru na równanie prostej prostopadłej do wektora
można bardzo szybko napisać korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/5425996/HzadR37x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 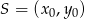 :
:
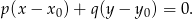
W naszej sytuacji mamy
![→ → v = AC = [8,4]](https://img.zadania.info/zad/5425996/HzadR40x.gif)
i 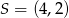 . Zatem prosta
. Zatem prosta 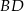 ma równanie
ma równanie
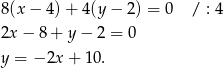
Współrzędne punktów 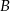 i
i 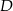 wyznaczamy jak w poprzednim sposobie.
wyznaczamy jak w poprzednim sposobie.
Odpowiedź: