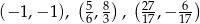/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 5522669

Dodaj do ulubionych
Dodaj do rozwiązanych

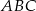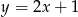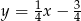Dwa boki trójkąta prostokątnego ABC są zawarte w prostych o równaniach y = 2x+ 1 oraz y = 14x − 34 . Wyznacz współrzędne wierzchołków trójkąta 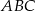ABC jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt 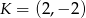K = (2,− 2) . Rozważ wszystkie możliwości.

Rozwiązanie

Zaczynamy od rysunku.

PIC

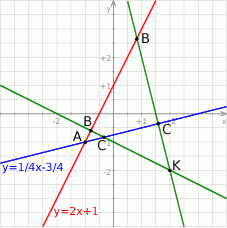
Na początek wyznaczmy punkt wspólny podanych prostych – jest to jeden z wierzchołków trójkąta, powiedzmy 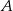A .

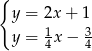
{ y = 2x + 1 1 3 y = 4x − 4

Odejmujemy od pierwszego równania drugie i mamy

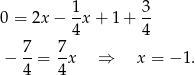
1 3 0 = 2x − --x+ 1+ -- 4 4 7- 7- − 4 = 4 x ⇒ x = − 1.

Stąd 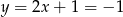y = 2x + 1 = − 1 i A = (− 1,− 1) .

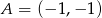Podane dwie proste nie są prostopadłe, więc szukana prosta, zawierająca trzeci bok trójkąta 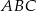ABC , musi być prostopadła do jednej z podanych prostych.

Na początek spróbujmy znaleźć prostą prostopadłą do prostej 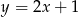y = 2x + 1 i przechodzącą przez punkt 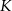K . Szukamy prostej w postaci 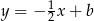y = − 12x+ b i podstawiamy współrzędne punktu K .

− 2 = −1 + b ⇒ b = − 1.

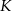Jest to więc prosta 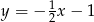y = − 1x − 1 2 . Szukamy punktów wspólnych tej prostej z danymi prostymi.

{ 1 { 1 y = − 2x − 1 y = − 2x − 1 y = 2x + 1 y = 14x − 34

Najpierw rozwiązujemy pierwszy układ – odejmujemy od drugiego równania pierwsze.

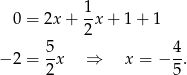
0 = 2x + 1x + 1 + 1 2 5 4 − 2 = -x ⇒ x = − -. 2 5

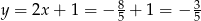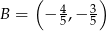Stąd y = 2x + 1 = − 8+ 1 = − 3 5 5 i mamy punkt ( ) B = − 4,− 3 5 5 .

Teraz rozwiązujemy drugi układ – odejmujemy od drugiego równania pierwsze.

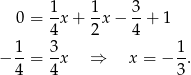
0 = 1x + 1-x − 3-+ 1 4 2 4 1- 3- 1- − 4 = 4x ⇒ x = − 3 .

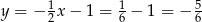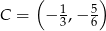Stąd y = − 1x − 1 = 1 − 1 = − 5 2 6 6 i ( ) C = − 1,− 5 3 6 .

Teraz zajmujemy się drugą możliwością, gdy trzeci bok trójkąta jest prostopadły do prostej 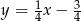y = 14 x− 34 . Szukamy teraz prostej w postaci 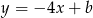y = − 4x+ b i podstawiamy współrzędne punktu K .

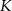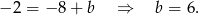
− 2 = −8 + b ⇒ b = 6.

Trzeci bok trójkąta ma w tym przypadku równanie 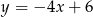y = − 4x + 6 . Tak jak poprzednio szukamy punktów wspólnych tej prostej z dwoma podanymi prostymi.

{ { y = − 4x + 6 y = − 4x+ 6 y = 2x + 1 y = 14x − 34

Rozwiązujemy najpierw pierwszy układ – odejmujemy od drugiego równania pierwsze.

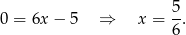
0 = 6x− 5 ⇒ x = 5. 6

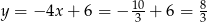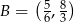Stąd y = − 4x + 6 = − 130+ 6 = 83 i ( ) B = 56, 83 .

Teraz rozwiązujemy drugi układ – odejmujemy od drugiego równania pierwsze.

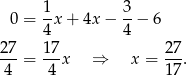
1- 3- 0 = 4 x+ 4x− 4 − 6 27 17 27 ---= ---x ⇒ x = --. 4 4 17

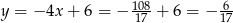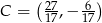Stąd 108 6- y = − 4x + 6 = − 17 + 6 = − 17 i (27 6-) C = 17,− 17 .  
Odpowiedź: 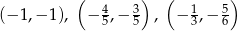( ) ( ) (− 1,− 1), − 4,− 3 , − 1,− 5 5 5 3 6 lub (5 8) ( 27 6 ) (− 1,− 1), 6,3 , 17,− 17

Wersja PDF