Zadanie nr 5633827
Mając dane współrzędne punktu 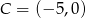 kwadratu
kwadratu 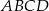 oraz współrzędne punktu przecięcia się przekątnych
oraz współrzędne punktu przecięcia się przekątnych 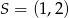 , wyznacz współrzędne pozostałych wierzchołków kwadratu
, wyznacz współrzędne pozostałych wierzchołków kwadratu  .
.
Rozwiązanie
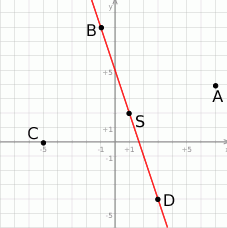
Ze wzoru na środek odcinka od razu wyliczamy współrzędne punktu 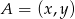 .
.
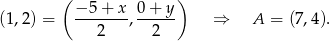
Jak wyznaczyć pozostałe wierzchołki? Jest na to wiele sposobów, jeden z najprostszych to napisanie równania drugiej przekątnej kwadratu i znalezienie na niej punktów, które są odległe od 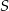 o tyle samo co
o tyle samo co 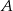 i
i 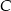 . Policzmy najpierw odległość
. Policzmy najpierw odległość 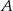 i
i 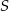 .
.
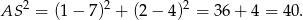
Aby napisać równanie drugiej przekątnej skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/5633827/HzadR9x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 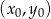
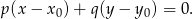
W naszej sytuacji ![→ → v = AS = [− 6,− 2]](https://img.zadania.info/zad/5633827/HzadR12x.gif) , czyli prosta
, czyli prosta 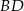 ma równanie
ma równanie
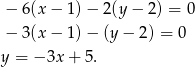
Szukamy teraz na tej prostej punktów, których kwadrat odległości od 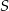 wynosi
wynosi 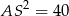 .
.
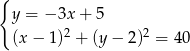
Podstawiając za 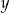 w drugim równaniu mamy
w drugim równaniu mamy
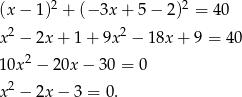
Liczymy 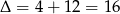 ,
, 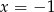 lub
lub 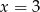 . Stąd
. Stąd 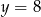 i
i 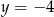 odpowiednio.
odpowiednio.
Odpowiedź: 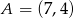 ,
, 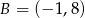 ,
,