Zadanie nr 5650662
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 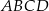 jeżeli
jeżeli 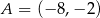 ,
, 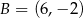 ,
, 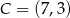 i
i 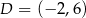 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
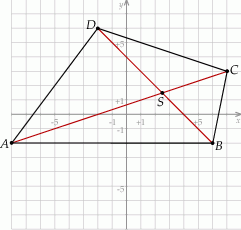
Aby wyznaczyć współrzędne punktu 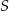 napiszemy równania prostych
napiszemy równania prostych 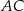 i
i 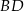 , a potem znajdziemy ich punkt wspólny.
, a potem znajdziemy ich punkt wspólny.
Równania prostych 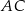 i
i 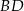 można napisać korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale my nie będziemy z niego korzystać.
można napisać korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale my nie będziemy z niego korzystać.
Najpierw prosta 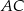 : szukamy prostej w postaci
: szukamy prostej w postaci 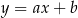 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 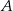 i
i 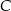
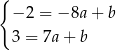
Odejmujemy od drugiego równania pierwsze (żeby zredukować 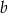 ) i mamy
) i mamy
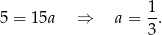
Zatem 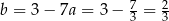 i prosta
i prosta 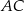 mam równanie
mam równanie 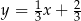 .
.
Dokładnie w ten sam sposób wyznaczamy równanie prostej 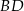 : podstawiamy do wzoru
: podstawiamy do wzoru 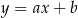 współrzędne punktów
współrzędne punktów 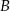 i
i 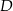 .
.
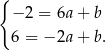
Odejmujemy od pierwszego równania drugie i mamy
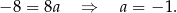
Zatem 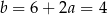 i prosta
i prosta 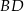 ma równanie
ma równanie 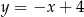 .
.
Teraz pozostało znaleźć punkt wspólny prostych 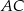 i
i 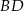 .
.
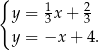
Podstawiamy 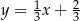 z pierwszego równania do drugiego
z pierwszego równania do drugiego
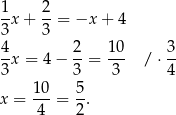
Stąd 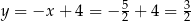 i
i 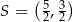 .
.
Odpowiedź: