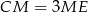Zadanie nr 5653439
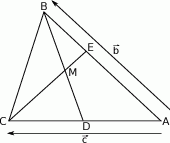
Na bokach 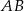 i
i 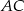 trójkąta
trójkąta 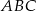 wybrano punkty
wybrano punkty 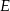 i
i 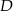 w ten sposób, że
w ten sposób, że 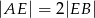 i
i 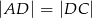 . Punkt
. Punkt 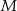 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 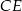 i
i 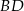 .
.
- Przedstaw każdy z wektorów
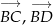 oraz
oraz 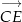 w postaci
w postaci 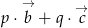 , gdzie
, gdzie 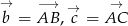 oraz
oraz 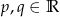 .
. - Korzystając z równości
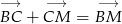 oblicz w jakim stosunku punkt
oblicz w jakim stosunku punkt 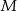 dzieli odcinki
dzieli odcinki 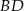 i
i 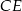 .
.
Rozwiązanie
- Liczymy
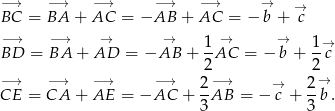
Odpowiedź: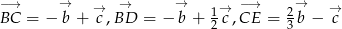
- Powiedzmy, że
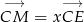 i
i 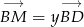 . Wstawiając te wyrażenia do podanej równości i korzystając z poprzedniego podpunktu mamy
. Wstawiając te wyrażenia do podanej równości i korzystając z poprzedniego podpunktu mamy 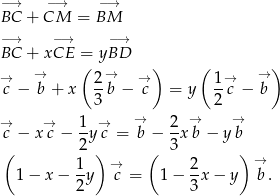
Wektory
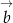 i
i 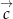 nie są jednak równoległe, co oznacza, że liczby w nawiasach w powyższej równości muszą być równe 0 (inaczej jeden wektor byłby wielokrotnością drugiego, co nie jest możliwe). Mamy stąd
nie są jednak równoległe, co oznacza, że liczby w nawiasach w powyższej równości muszą być równe 0 (inaczej jeden wektor byłby wielokrotnością drugiego, co nie jest możliwe). Mamy stąd 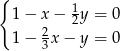
Podstawiamy
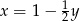 z pierwszego równania do drugiego i mamy
z pierwszego równania do drugiego i mamy 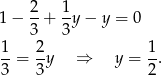
Zatem
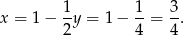
Mamy więc
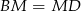 i
i 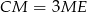 .
.
Odpowiedź: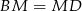 i
i