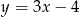Zadanie nr 5654966
Wyznacz równanie prostej przechodzącej przez punkty  i
i 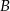 jeżeli
jeżeli 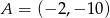 i
i 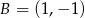 .
.
Rozwiązanie
Możemy zacząć od naszkicowania o co chodzi.
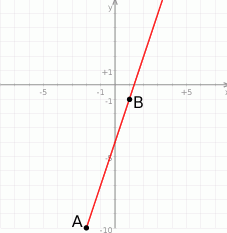
Sposób I
Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty:
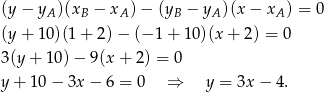
Sposób II
Szukamy prostej w postaci 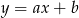 . Podstawiając podane punkty dostajemy układ równań
. Podstawiając podane punkty dostajemy układ równań
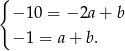
Odejmując od pierwszego równania drugie (żeby skrócić 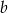 ), mamy
), mamy

Z drugiego równania mamy 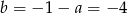 .
.
Odpowiedź: