/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 5773019

Dodaj do ulubionych
Dodaj do rozwiązanych

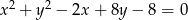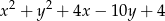Określ wzajemne położenie okręgów 2 2 x + y − 2x + 8y − 8 = 0 i x 2 + y2 + 4x − 1 0y+ 4 .

Rozwiązanie

Możemy dokładnie narysować podane okręgi (cyrklem) i sprawdzić jakie jest ich wzajemne położenie.

PIC

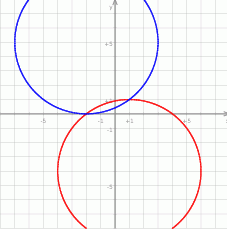
Czasami jednak trudno jest z rysunku ustalić dokładne położenie i dlatego skupimy się na metodach rachunkowych.

Sposób I

Najwygodniej jest skorzystać z następującej charakteryzacji wzajemnego położenia dwóch okręgów o środkach 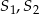S1,S2 i promieniach R 1 > R 2 .

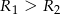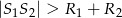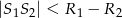  • Jeżeli |S 1S2| > R 1 + R 2 lub |S1S 2| < R 1 − R2 to okręgi są rozłączne (nie przecinają się)
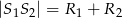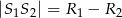  • Jeżeli |S1S2| = R 1 + R2 lub |S1S2| = R 1 − R2 to okręgi są styczne (przecinają się w jednym punkcie)
  • Jeżeli 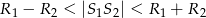R1 − R 2 < |S1S2| < R 1 + R 2 to okręgi przecinają się w dwóch punktach.

Jeżeli promienie okręgów są równe, to jest jeden dodatkowy wyjątek: jeżeli 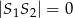|S1S 2| = 0 to okręgi pokrywają się.

Przekształćmy równanie pierwszego okręgu (żeby zobaczyć jaki ma środek i promień).

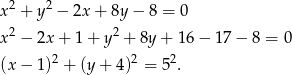
2 2 x + y − 2x + 8y − 8 = 0 x2 − 2x + 1 + y2 + 8y + 16 − 17 − 8 = 0 2 2 2 (x − 1) + (y + 4) = 5 .

Jest to więc okrąg o środku 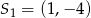S1 = (1,− 4) i promieniu 5.

Podobnie przekształćmy drugie równanie.

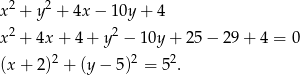
x 2 + y 2 + 4x − 10y + 4 2 2 x + 4x + 4+ y − 10y+ 25 − 29 + 4 = 0 (x + 2 )2 + (y − 5)2 = 52.

Jest to więc okrąg o środku 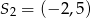S2 = (− 2,5) i promieniu 5. Mamy więc

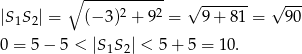
∘ ----------- √ ------- √ --- |S1S 2| = (− 3)2 + 92 = 9+ 81 = 90 0 = 5− 5 < |S1S2| < 5 + 5 = 10 .

Zatem okręgi przecinają się w dwóch punktach.

Sposób II

Zadanie można też rozwiązać czysto algebraicznie. Wprawdzie rozwiązanie to jest bardziej skomplikowane rachunkowo, ale za to pozwoli dokładnie wyliczyć ewentualne punkty wspólne danych okręgów.

Musimy sprawdzić ile rozwiązań ma układ równań

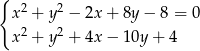
{ x2 + y2 − 2x + 8y − 8 = 0 x2 + y2 + 4x − 10y + 4

Odejmując od pierwszego równania drugie (żeby skrócić kwadraty) mamy

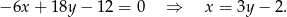
− 6x + 18y − 12 = 0 ⇒ x = 3y − 2.

Podstawiamy to do pierwszego równania

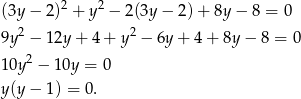
(3y − 2)2 + y 2 − 2 (3y− 2)+ 8y− 8 = 0 2 2 9y − 12y + 4+ y − 6y + 4+ 8y − 8 = 0 1 0y2 − 10y = 0 y (y− 1) = 0.

Ponieważ układ ten ma dwa rozwiązania, okręgi przecinają się w dwóch punktach.  
Odpowiedź: Okręgi przecinają się w dwóch punktach

Wersja PDF