Zadanie nr 5831161
Na hiperboli 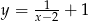 wyznacz taki punkt
wyznacz taki punkt 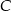 , który jest równoodległy od punktów
, który jest równoodległy od punktów 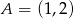 i
i 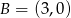 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku. Hiperbola 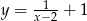 powstaje z hiperboli
powstaje z hiperboli 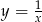 przez przesunięcie o wektor
przez przesunięcie o wektor ![[2,1 ]](https://img.zadania.info/zad/5831161/HzadR2x.gif) .
.
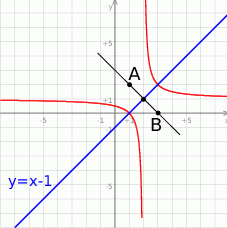
Plan jest następujący: napiszemy równanie symetralnej odcinka 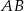 i znajdziemy jej punkty wspólne z daną hiperbolą (widać, że będą dwa takie punkty).
i znajdziemy jej punkty wspólne z daną hiperbolą (widać, że będą dwa takie punkty).
Środek odcinka 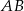 ma współrzędne
ma współrzędne 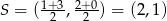 . Teraz najłatwiej skorzystać ze wzoru na równanie prostej prostopadłej do wektora
. Teraz najłatwiej skorzystać ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/5831161/HzadR7x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 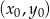 :
:
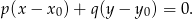
W naszej sytuacji ![→ → v = AB = [2,− 2]](https://img.zadania.info/zad/5831161/HzadR10x.gif) , a punkt to środek
, a punkt to środek 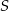 odcinka
odcinka 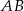 . Zatem symetralna odcinka
. Zatem symetralna odcinka 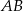 ma równanie
ma równanie
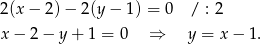
Pozostało znaleźć punkty wspólne tej prostej z daną hiperbolą.
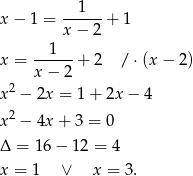
Daje to nam dwa punkty 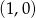 i
i 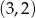 (bo
(bo 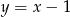 ).
).
Odpowiedź: 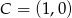 lub
lub