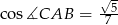Zadanie nr 6091486
W trójkącie 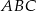 dane są
dane są 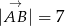 ,
, 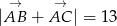 oraz
oraz 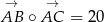 . Oblicz długość boku
. Oblicz długość boku 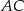 , oraz miarę kąta
, oraz miarę kąta 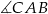 .
.
Rozwiązanie
Zacznijmy od rysunku i oznaczmy 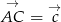 oraz
oraz 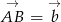 .
.
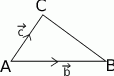
Mamy zatem 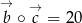 oraz
oraz
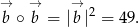
Ponadto
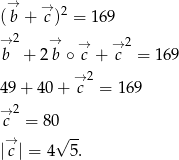
Cosinus kąta 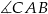 wyliczymy ze wzoru
wyliczymy ze wzoru
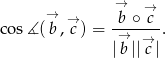
Mamy zatem
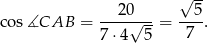
Odpowiedź: 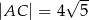 ,
, 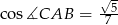
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 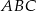 dane są
dane są 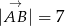 ,
, 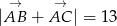 oraz
oraz 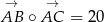 . Oblicz długość boku
. Oblicz długość boku 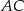 , oraz miarę kąta
, oraz miarę kąta 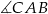 .
.
Zacznijmy od rysunku i oznaczmy 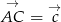 oraz
oraz 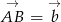 .
.

Mamy zatem 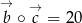 oraz
oraz
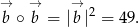
Ponadto
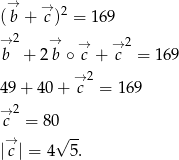
Cosinus kąta 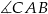 wyliczymy ze wzoru
wyliczymy ze wzoru
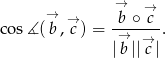
Mamy zatem
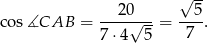
Odpowiedź: 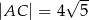 ,
,