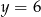/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6101909

Dodaj do ulubionych
Dodaj do rozwiązanych

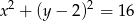Wyznacz równanie prostej prostopadłej do wektora → u = [0,− 3] i stycznej do okręgu x2 + (y − 2)2 = 16 .

Rozwiązanie

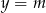Wektor [0,− 3] jest pionowy, więc proste prostopadłe do niego, to proste postaci y = m . Pozostało sprawdzić, kiedy taka prosta jest styczna do podanego okręgu.

Sposób I

Spróbujmy narysować podany okrąg – jest to okrąg o środku 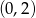(0,2) i promieniu 4. Z rysunku widać, że prosta 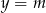y = m jest do niego styczna jeżeli 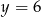y = 6 lub − 2 .

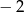Sposób II

PIC

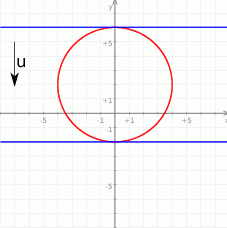
Jeżeli kogoś nie przekonują obrazki, to może sobie to wyliczyć. Wstawiamy 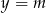y = m do równania okręgu i sprawdzamy kiedy jest dokładnie jeden punkt wspólny (bo ten warunek charakteryzuje styczne).

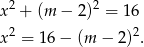
x2 + (m − 2)2 = 16 2 2 x = 1 6− (m − 2) .

Aby to równanie miało dokładnie jedno rozwiązanie, prawa strona musi być równa 0 (bo jak jest ujemna to wcale nie ma rozwiązań, a jak jest dodatnia to są dwa). Zatem

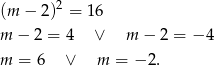
(m − 2)2 = 16 m − 2 = 4 ∨ m − 2 = −4 m = 6 ∨ m = − 2.

Sposób III

Podobnie jak poprzednio sprawdźmy, kiedy prosta 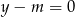y − m = 0 jest styczna do danego okręgu. Tak będzie gdy środek okręgu będzie od niej odległy o 4 (promień okręgu). Liczymy (korzystamy ze wzoru na odległość punktu od prostej).

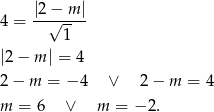
|2−--m|- 4 = √ -- 1 |2 − m | = 4 2 − m = − 4 ∨ 2 − m = 4 m = 6 ∨ m = − 2.

 
Odpowiedź: 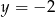y = − 2 lub y = 6

Wersja PDF