Zadanie nr 6104846
W prostokącie 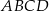 dane są
dane są 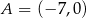 ,
, 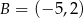 i
i 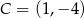 . Napisz równanie prostej, która jest styczna w punkcie
. Napisz równanie prostej, która jest styczna w punkcie 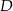 do okręgu opisanego na prostokącie
do okręgu opisanego na prostokącie 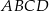 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
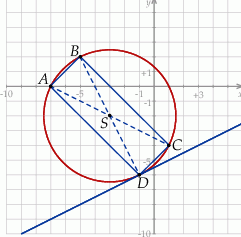
Wyznaczmy najpierw współrzędne czwartego wierzchołka prostokąta. Środek 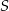 prostokąta ma współrzędne
prostokąta ma współrzędne
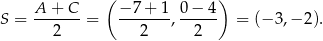
Punkt 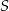 jest też środkiem odcinka
jest też środkiem odcinka 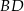 . Stąd
. Stąd
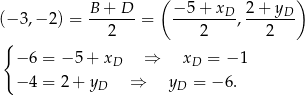
Zatem 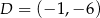 . Równanie stycznej do okręgu w punkcie
. Równanie stycznej do okręgu w punkcie 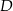 napiszemy jako równanie prostej przechodzącej przez
napiszemy jako równanie prostej przechodzącej przez 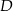 i prostopadłej do promienia
i prostopadłej do promienia 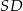 . Najpierw piszemy równanie prostej
. Najpierw piszemy równanie prostej 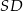 . Szukamy prostej w postaci
. Szukamy prostej w postaci 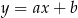 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 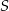 i
i 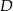 .
.
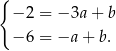
Odejmujemy od drugiego równania pierwsze (żeby skrócić 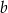 ) i mamy
) i mamy
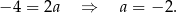
Współczynnika 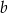 nie potrzebujemy, więc możemy go nie obliczać.
nie potrzebujemy, więc możemy go nie obliczać.
Szukana styczna jest prostopadła do 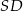 , więc ma równanie postaci
, więc ma równanie postaci 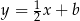 . Współczynnik
. Współczynnik 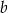 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 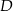 .
.
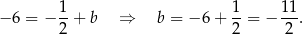
Szukana styczna ma więc równanie 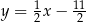 .
.
Odpowiedź: