/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6140922

Dodaj do ulubionych
Dodaj do rozwiązanych

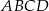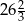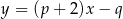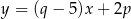Przekątne prostokąta ABCD o obwodzie 2 26 3 są zawarte w prostych o równaniach y = (p + 2)x − q i y = (q− 5)x + 2p . Ponadto prosta 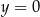y = 0 jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

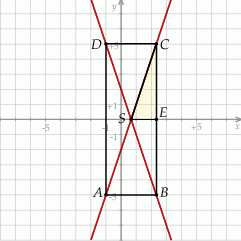
Zauważmy najpierw, że podana oś symetrii prostokąta nie zawiera jego przekątnej – rzeczywiście, w takiej sytuacji 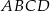ABCD jest kwadratem i druga z przekątnych byłaby pionowa, a żadna z podanych prostych nie jest pionowa. W takim razie podana oś symetrii przechodzi przez środki przeciwległych boków prostokąta i zamienia jego przekątne ze sobą. Obrazem prostej 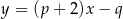y = (p+ 2)x − q w symetrii względem osi 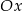Ox jest prosta 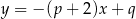y = −(p + 2)x+ q i musi to być ta sama prosta, co 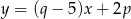y = (q − 5)x + 2p . Mamy stąd układ równań

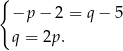
{ −p − 2 = q − 5 q = 2p .

Podstawiamy z drugiego równania do pierwszego i mamy

−p − 2 = 2p − 5 ⇒ 3p = 3 ⇒ p = 1.

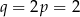Stąd q = 2p = 2 i przekątne prostokąta mają równania

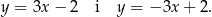
y = 3x − 2 i y = − 3x+ 2.

Wyznaczmy punkt wspólny tych prostych, czyli środek 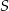S prostokąta.

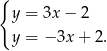
{ y = 3x − 2 y = − 3x + 2.

Dodajemy równania układu stronami i otrzymujemy 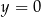y = 0 . Stąd 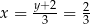x = y+2-= 2 3 3 i (2 ) S = 3,0 .

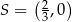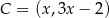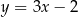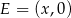Używając oznaczeń z powyższego rysunku, niech C = (x ,3x− 2) będzie punktem prostej y = 3x − 2 i E = (x,0) niech będzie środkiem odcinka 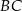BC . Mamy wtedy

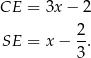
CE = 3x − 2 SE = x − 2-. 3

Z drugiej strony wiemy, że

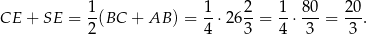
1 1 2 1 80 20 CE + SE = -(BC + AB ) = --⋅26--= --⋅---= ---. 2 4 3 4 3 3

To prowadzi do równania

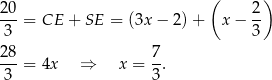
20 ( 2) ---= CE + SE = (3x − 2)+ x− -- 3 3 28- 7- 3 = 4x ⇒ x = 3.

Przy oznaczeniach z naszego rysunku mamy więc

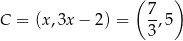
( 7 ) C = (x,3x − 2) = -,5 3

i

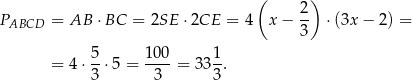
( ) PABCD = AB ⋅BC = 2SE ⋅2CE = 4 x− 2- ⋅ (3x− 2) = 3 5 100 1 = 4 ⋅--⋅5 = ----= 3 3-. 3 3 3

 
Odpowiedź: 100 1 3 = 33 3

Wersja PDF