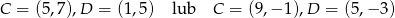Zadanie nr 6250343
Punkt 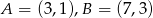 są kolejnymi wierzchołkami kwadratu
są kolejnymi wierzchołkami kwadratu 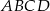 . Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
Rozwiązanie
Zaczynamy od rysunku
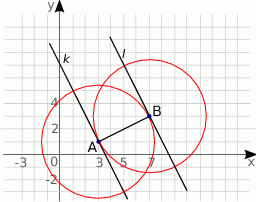
Wyznaczymy równania prostych prostopadłych przechodzących przez punkt 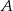 i
i 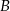 (na rysunku oznaczone przez
(na rysunku oznaczone przez 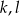 ), a następnie na każdej z tych prostych znajdziemy punkty które są w takiej samej odległości od punktu
), a następnie na każdej z tych prostych znajdziemy punkty które są w takiej samej odległości od punktu 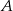 (odpowiednio
(odpowiednio 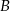 ) co punkt
) co punkt 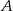 od punktu
od punktu 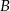 . Najpierw wyznaczymy pomocniczą prostą przechodzącą przez punkty
. Najpierw wyznaczymy pomocniczą prostą przechodzącą przez punkty 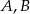
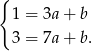
Odejmujemy stronami równania
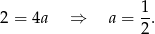
Stąd
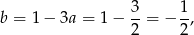
czyli 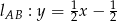 . Niech
. Niech
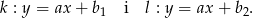
Obydwie powyższe proste są prostopadłe do 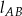 , więc
, więc
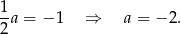
Wyznaczamy prostą 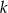
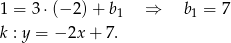
Wyznaczamy prostą 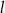
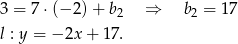
Liczymy odległość punktu  od
od 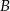
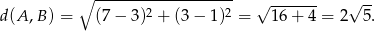
Gdybyśmy mieli teraz geometrycznie wyznaczyć pozostałe punkty, to wystarczyło by narysować okręgi o środkach w punktach  i
i  i promieniu
i promieniu 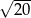 . Wówczas szukanymi punktami byłyby punkty przecięcia się tych okręgów z prostymi
. Wówczas szukanymi punktami byłyby punkty przecięcia się tych okręgów z prostymi 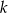 i
i 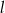 . My zrobimy dokładnie to samo tyle, że używając rachunków. Okrąg o środku w punkcie
. My zrobimy dokładnie to samo tyle, że używając rachunków. Okrąg o środku w punkcie 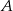 i promieniu
i promieniu 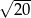 ma równanie
ma równanie
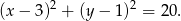
Wyznaczmy punkty wspólne tego okręgu i prostej 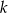
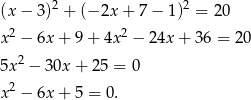
Liczymy pierwiastki
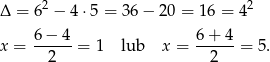
Zatem
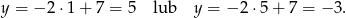
Okrąg o środku w punkcie 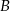 i promieniu
i promieniu 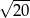 ma równanie
ma równanie
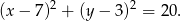
Wyznaczmy punkty wspólne tego okręgu i prostej 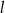
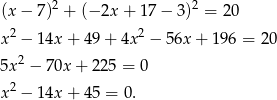
Liczymy pierwiastki
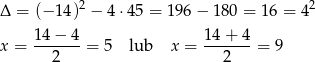
Zatem
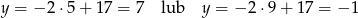
Podsumowując otrzymujemy dwa warianty dla pozostałych punktów
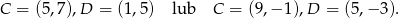
Odpowiedź: