/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6365221

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeden z końców odcinka leży na paraboli 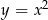2 y = x , a drugi na prostej o równaniu 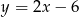y = 2x− 6 . Wykaż, że długość tego odcinka jest nie mniejsza od 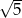√ -- 5 . Sporządź odpowiedni rysunek.

Rozwiązanie

Możemy na początku sobie naszkicować o co chodzi.

PIC

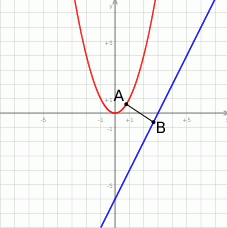
W pierwszej chwili można by pomyśleć tak: bierzemy punkt 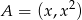A = (x,x2) z paraboli i punkt 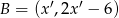B = (x′,2x′ − 6 ) z prostej i musimy pokazać, że są odległe o co najmniej 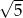√ 5- . Tak jednak będzie trudno to rozwiązać, bo mamy dwa parametry.

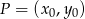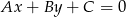Żeby mieć jeden parametr korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

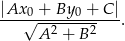
|Ax-0√-+-By-0 +-C|. A 2 + B 2

W naszej sytuacji bierzemy punkt 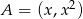A = (x ,x2) na paraboli i daną prostą. Liczymy

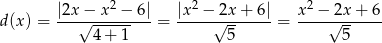
|2x − x2 − 6| |x2 − 2x + 6| x2 − 2x+ 6 d(x) = --√----------= -----√------- = ----√------- 4+ 1 5 5

(opuściliśmy wartość bezwzględną, bo 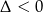Δ < 0 ).

Teraz mamy różne możliwości.

Możemy zauważyć, że

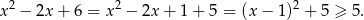
x2 − 2x + 6 = x2 − 2x+ 1+ 5 = (x − 1)2 + 5 ≥ 5.

Możemy też wyliczyć najmniejszą wartość funkcji 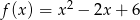f (x) = x2 − 2x + 6 ze wzorów na wierzchołek paraboli.

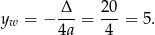
Δ 20 yw = − ---= ---= 5. 4a 4

Możemy wreszcie pokazać, że zachodzi nierówność

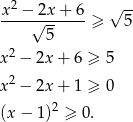
x2 − 2x + 6 √ -- ----√-------≥ 5 5 x2 − 2x + 6 ≥ 5 2 x − 2x + 1 ≥ 0 (x − 1)2 ≥ 0.

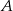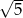Niezależnie od wybranego sposobu dostajemy, że odległość punktu A od podanej prostej jest równa co najmniej √ -- 5 .

Wersja PDF