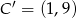Zadanie nr 6390962
Trójkąt o wierzchołkach 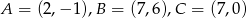 przekształcono w jednokładności o skali
przekształcono w jednokładności o skali 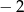 i otrzymano trójkąt o wierzchołkach
i otrzymano trójkąt o wierzchołkach  . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 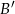 i
i 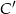 jeżeli
jeżeli 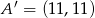 .
.
Rozwiązanie
Na początku trudno zrobić dokładny rysunek, więc szkicujemy opisaną sytuację.
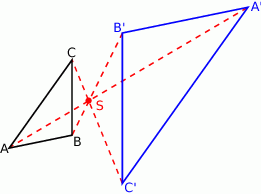
Zauważmy, że znając skalę jednokładności oraz współrzędne punktów  i
i 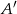 łatwo jest wyznaczyć środek
łatwo jest wyznaczyć środek 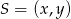 jednokładności. Z definicji jednokładności mamy
jednokładności. Z definicji jednokładności mamy
![−→ ′ −→ SA = −2 ⋅SA [11 − x ,11− y] = − 2[2− x,− 1− y] { 11 − x = − 4 + 2x ⇒ x = 5 11 − y = 2 + 2y ⇒ y = 3](https://img.zadania.info/zad/6390962/HzadR4x.gif)
Zatem 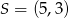 . Wyznaczamy teraz współrzędne punktu
. Wyznaczamy teraz współrzędne punktu 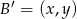 .
.
![−→ −→ SB′ = − 2 ⋅SB [x − 5 ,y − 3 ] = −2 [7 − 5,6 − 3] { x − 5 = − 4 ⇒ x = 1 y − 3 = − 6 ⇒ y = − 3.](https://img.zadania.info/zad/6390962/HzadR7x.gif)
Zatem 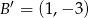 . Teraz wyznaczamy współrzędne punktu
. Teraz wyznaczamy współrzędne punktu 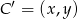 .
.
![−→′ −→ SC = − 2⋅ SC [x − 5,y − 3] = − 2[7− 5,0 − 3] { x − 5 = − 4 ⇒ x = 1 y − 3 = 6 ⇒ y = 9 .](https://img.zadania.info/zad/6390962/HzadR10x.gif)
Zatem 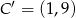 .
.
Na koniec dokładny rysunek sytuacji opisanej w zadaniu.
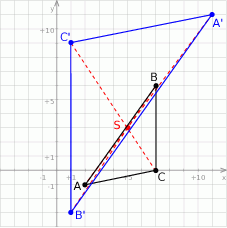
Odpowiedź: 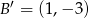 ,
,