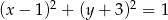/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6415727

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź równanie okręgu o środku w punkcie 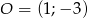O = (1;− 3) , wiedząc, że okrąg jest styczny do prostej x = 2 .

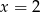Rozwiązanie

Jeżeli naszkicujemy opisaną sytuację to widać, że długość promienia szukanego okręgu jest równa odległości punktu 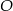O od prostej 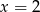x = 2 , czyli jest równa 1.

PIC

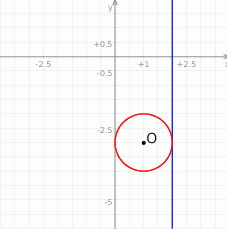
Zatem szukane równanie ma postać

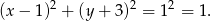
(x − 1 )2 + (y + 3)2 = 12 = 1.

 
Odpowiedź: (x − 1)2 + (y + 3)2 = 1

Wersja PDF