Zadanie nr 6463995
Trapez równoramienny 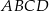 o podstawach
o podstawach 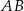 i
i 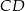 jest opisany na okręgu o równaniu
jest opisany na okręgu o równaniu 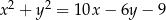 . Okrąg ten przecina boki
. Okrąg ten przecina boki 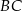 i
i 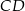 tego trapezu odpowiednio w punktach
tego trapezu odpowiednio w punktach 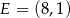 i
i 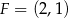 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 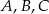 i
i 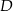 tego trapezu.
tego trapezu.
Rozwiązanie
Przekształćmy najpierw równanie danego okręgu tak, żeby było widać jaki jest jego środek i promień.
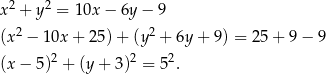
Jest to więc okrąg o środku 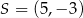 i promieniu
i promieniu 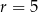 . Szkicujemy opisaną sytuację.
. Szkicujemy opisaną sytuację.
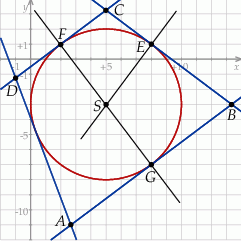
Trapez równoramienny posiada oś symetrii – jest to prosta przechodząca przez środki 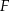 i
i 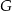 podstaw
podstaw 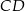 i
i 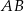 . Prosta ta jest też oczywiście osią symetrii okręgu wpisanego w trapez, więc
. Prosta ta jest też oczywiście osią symetrii okręgu wpisanego w trapez, więc 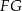 jest średnicą tego okręgu. To pozwala łatwo łatwo wyznaczyć współrzędne punktu
jest średnicą tego okręgu. To pozwala łatwo łatwo wyznaczyć współrzędne punktu 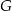 .
.
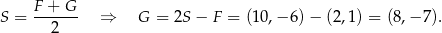
W kolejnym kroku napiszemy równania podstaw 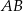 i
i 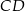 – są to proste prostopadłe do
– są to proste prostopadłe do 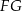 i przechodzące odpowiednio przez
i przechodzące odpowiednio przez 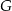 i
i 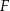 . Zanim to jednak zrobimy, wyznaczmy współczynnik kierunkowy prostej
. Zanim to jednak zrobimy, wyznaczmy współczynnik kierunkowy prostej 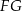 . Szukamy prostej w postaci
. Szukamy prostej w postaci 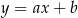 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 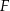 i
i 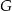 .
.
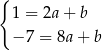
Odejmujemy od pierwszego równania drugie i mamy
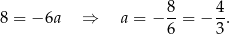
W takim razie każda z podstaw 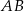 i
i 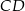 ma równanie postaci
ma równanie postaci 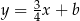 . Podstawiamy najpierw współrzędne punktu
. Podstawiamy najpierw współrzędne punktu 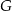 .
.
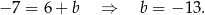
Podstawa 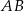 ma więc równanie
ma więc równanie 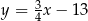 . Teraz podstawiamy współrzędne punktu
. Teraz podstawiamy współrzędne punktu 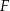 .
.
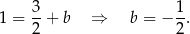
Podstawa 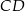 ma więc równanie
ma więc równanie 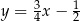 .
.
Teraz wyznaczymy równanie prostej 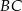 – jest to prosta prostopadła do
– jest to prosta prostopadła do 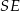 i przechodząca przez
i przechodząca przez 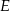 . Możemy to zrobić dokładnie tak samo jak wcześniej – pisząc najpierw równanie prostej
. Możemy to zrobić dokładnie tak samo jak wcześniej – pisząc najpierw równanie prostej 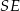 . Dla urozmaicenia zrobimy to jednak prościej – korzystamy ze wzoru na równanie prostej prostopadłej do wektora
. Dla urozmaicenia zrobimy to jednak prościej – korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/6463995/HzadR37x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 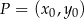
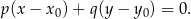
W naszej sytuacji mamy
![→v = −S→E = E − S = [8 − 5 ,1 + 3 ] = [3,4]](https://img.zadania.info/zad/6463995/HzadR40x.gif)
i 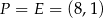 . Prosta
. Prosta 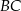 ma więc równanie
ma więc równanie
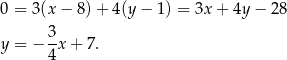
Szukamy teraz punktu wspólnego 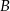 tej prostej i prostej
tej prostej i prostej 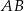 .
.
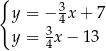
Odejmujemy od drugiego równania pierwsze i mamy
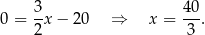
Stąd 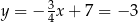 i
i 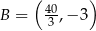 .
.
Teraz szukamy punktu wspólnego 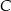 prostych
prostych 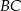 i
i 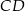 .
.
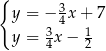
Odejmujemy od drugiego równania pierwsze i mamy
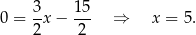
Stąd 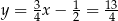 i
i 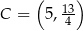 .
.
Teraz już jest łatwo – punkty 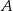 i
i 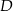 wyznaczamy ze wzoru na środek odcinka.
wyznaczamy ze wzoru na środek odcinka.
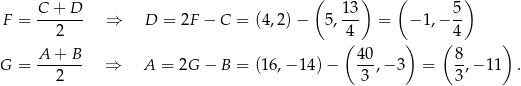
Odpowiedź: 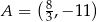 ,
, 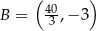 ,
, 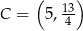 ,
,