/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6521220

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest odcinek o końcach 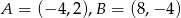A = (− 4,2 ),B = (8,− 4) .

  1. Wyznacz równanie okręgu o średnicy AB .
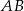  2. Wyznacz równanie średnicy prostopadłej do średnicy AB .

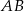Rozwiązanie

Rozpoczynamy od rysunku.

PIC

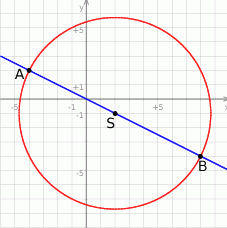
  • Środkiem okręgu będzie środek odcinka 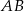AB . Liczymy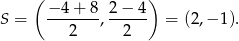
    ( − 4+ 8 2 − 4) S = -------,------ = (2,− 1). 2 2

    Promień będzie równy odległości punktu 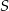S od punktu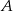 A

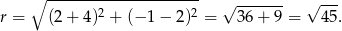
    ∘ --------------------- √ ------- √ --- r = (2+ 4)2 + (− 1 − 2)2 = 36+ 9 = 45.

    Zatem szukany okrąg ma równanie

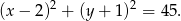
    (x − 2)2 + (y + 1)2 = 45.

     
    Odpowiedź: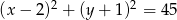 2 2 (x − 2) + (y + 1) = 45

  • Wyznaczamy współczynnik kierunkowy prostej przechodzącej przez punkty AB
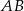
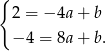
    { 2 = − 4a + b − 4 = 8a + b.

    Odejmujemy równania stronami i otrzymujemy

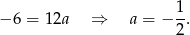
    1 − 6 = 12a ⇒ a = − -. 2

    Zatem współczynnik kierunkowy 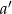′ a szukanej prostej wynosi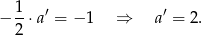

    − 1-⋅a′ = − 1 ⇒ a′ = 2. 2

    Szukana prosta ma zawierać średnicę, więc musi przechodzić przez środek okręgu

    −1 = 2⋅2 + b ⇒ b = − 5.

    Stąd szukana prosta ma równanie

    y = 2x − 5 .

     
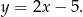
    Odpowiedź: y = 2x − 5

Wersja PDF