/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6549643

Dodaj do ulubionych
Dodaj do rozwiązanych

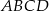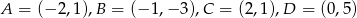Oblicz pole czworokąta ABCD , którego wierzchołki mają współrzędne A = (− 2,1),B = (− 1,− 3),C = (2,1),D = (0,5) .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

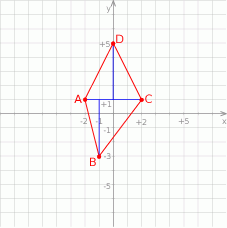
Sposób I

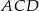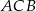Zauważmy, że interesujący nas czworokąt składa się dwóch trójkątów ACD i ACB o wspólnej podstawie 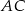AC długości

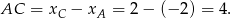
AC = xC − xA = 2 − (− 2) = 4.

Łatwo też policzyć wysokości tych trójkątów. Wysokość trójkąta 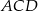ACD jest równa

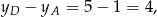
yD − yA = 5− 1 = 4,

a wysokość trójkąta 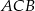ACB jest równa

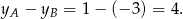
yA − yB = 1− (− 3 ) = 4.

Zatem pola tych trójkątów są odpowiednio równe

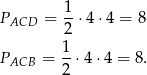
1 PACD = -⋅ 4⋅4 = 8 2 P = 1-⋅4 ⋅4 = 8 . ACB 2

Zatem pole całego czworokąta jest równe 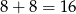8 + 8 = 16 .

Sposób II

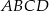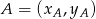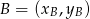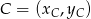Pole czworokąta ABCD możemy też obliczyć korzystając ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

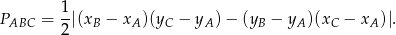
1 PABC = --|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|. 2

Mamy zatem

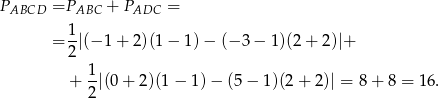
PABCD =PABC + PADC = = 1-|(− 1 + 2)(1 − 1) − (− 3 − 1)(2 + 2)|+ 2 1- + 2|(0 + 2)(1 − 1) − (5− 1)(2 + 2)| = 8+ 8 = 16.

 
Odpowiedź: 16

Wersja PDF