/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6609946

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że każdy punkt paraboli o równaniu 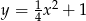1 2 y = 4x + 1 jest równoodległy od osi 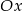Ox i od punktu F = (0,2) .

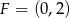Rozwiązanie

Po pierwsze naszkicujmy sobie tę parabolę.

PIC

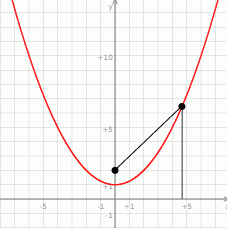
Jeżeli punkt 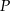P jest punktem podanej paraboli, to jest postaci 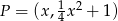P = (x, 14x 2 + 1 ) . Jego odległość od osi 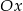Ox to po prostu druga współrzędna, czyli 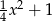1x2 + 1 4 (tu jest ważne, że parabola jest powyżej osi, czyli, że ta liczba jest dodatnia). Odległość tego punktu od 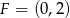F = (0,2) liczymy ze wzoru

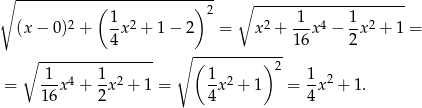
∘ -----------(-------------)-- ∘ --------------------- 1 2 1 1 (x − 0 )2 + 4-x2 + 1− 2 = x2 + 16-x4 − 2x 2 + 1 = ∘ ------------- ∘ 1------1-------- ( 1 ) 2 1 = --x 4 +--x2 + 1 = -x2 + 1 = -x 2 + 1. 16 2 4 4

Gdyby ktoś nie zauważył, że wyrażenie pod pierwiastkiem to pełen kwadrat to można po prostu porównać ten pierwiastek z tym co mam wyjść, czyli z 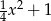1 x2 + 1 4 i przekształcać aż będzie 0=0.

Dla ciekawskich, każda parabola to zbiór punktów, które są równoodległe od pewnej prostej (zwanej kierownicą) i punktu (zwanego ogniskiem). W tym przykładzie kierownicą jest prosta 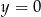y = 0 , a ogniskiem podany punkt 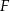F – dlatego zresztą się nazywa 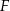F , od ’focal point’.

Wersja PDF