/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6639397

Dodaj do ulubionych
Dodaj do rozwiązanych

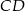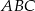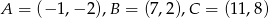Wyznacz równanie prostej zawierającej środkową CD trójkąta ABC , którego wierzchołkami są punkty: A = (− 1,− 2),B = (7,2),C = (11,8) .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

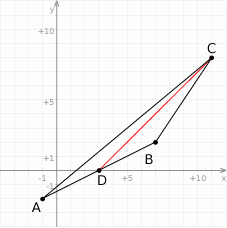
Punkt 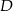D to środek odcinka 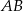AB , więc ma współrzędne

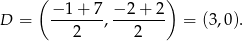
( ) D = −-1-+-7 , −-2+-2 = (3,0). 2 2

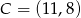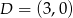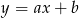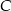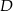Pozostało napisać równanie prostej przechodzącej przez punkty C = (11,8) i D = (3,0 ) . Można skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale można też wprost: szukamy prostej postaci y = ax+ b . Podstawiając współrzędne punktów C i D mamy układ równań

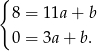
{ 8 = 11a + b 0 = 3a + b .

Odejmując od pierwszego równania drugie (żeby skrócić 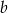b ) mamy

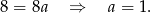
8 = 8a ⇒ a = 1.

Zatem 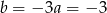b = − 3a = −3 .  
Odpowiedź: y = x− 3

Wersja PDF