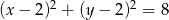Zadanie nr 6716451
Prosta 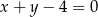 przecina oś
przecina oś 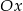 w punkcie
w punkcie 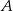 i oś
i oś 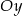 w punkcie
w punkcie 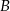 . Punkt
. Punkt 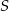 jest środkiem odcinka
jest środkiem odcinka 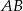 . Znajdź równanie okręgu o środku w punkcie
. Znajdź równanie okręgu o środku w punkcie 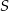 i promieniu
i promieniu 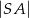 .
.
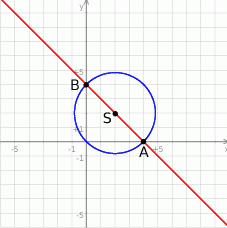
Rozwiązanie
Najpierw wyznaczamy współrzędne punktów 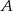 i
i 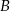 .
.
Punkt 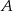 jest punktem przecięcia z osią
jest punktem przecięcia z osią 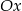 , więc jest postaci
, więc jest postaci 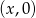 . Wyznaczamy go
. Wyznaczamy go
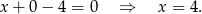
Ponieważ punkt 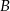 jest punktem przecięcia z osią
jest punktem przecięcia z osią 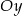 , więc jest postaci
, więc jest postaci 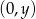 . Liczymy
. Liczymy
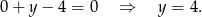
Wyznaczamy współrzędne środka
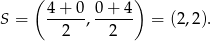
Zatem
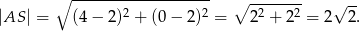
Stąd okrąg ma równanie
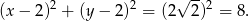
Odpowiedź: