/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6904754

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest okrąg o środku w punkcie 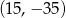(1 5,− 35) i promieniu 16. Sprawdź czy okrąg ten jest styczny do

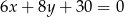  • prostej 6x + 8y + 30 = 0 ,
  • okręgu o środku w punkcie 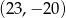(2 3,− 20) i promieniu 2?

Uzasadnij swoją odpowiedź.

Rozwiązanie

  • Okrąg jest styczny do prostej gdy odległość jego środka od tej prostej jest równa promieniowi okręgu.
    PIC

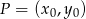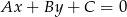    Policzmy tę odległość w naszej sytuacji. Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

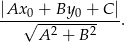
    |Ax 0 + By0 + C | ---√---2----2----. A + B

    Mamy więc

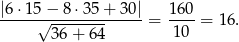
    |6 ⋅15 − 8⋅ 35+ 30| 16 0 -----√-------------- = ---- = 16. 36 + 6 4 10

    Zatem odpowiedź jest twierdząca.  
    Odpowiedź: Tak, jest styczny

  • Dwa okręgi są styczne gdy odległość ich środków jest równa sumie lub różnicy ich promieni (w zależności od tego czy okręgi są styczne zewnętrznie czy wewnętrznie). Policzmy tę odległość w naszej sytuacji.
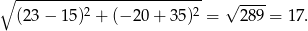
    ∘ -------------------------- √ ---- (23− 15)2 + (− 20+ 35)2 = 28 9 = 17.

     
    Odpowiedź: Nie, nie są

Wersja PDF