Zadanie nr 6905815
Sprawdź, czy czworokąt 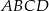 , gdzie
, gdzie 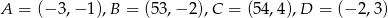 jest równoległobokiem. Odpowiedź uzasadnij.
jest równoległobokiem. Odpowiedź uzasadnij.
Rozwiązanie
Sposób I
Wystarczy sprawdzić, czy 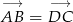 .
.
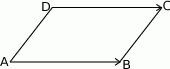
Liczymy
![−→ AB = [53+ 3,− 2+ 1] = [5 6,− 1] −→ DC = [54 + 2,4 − 3] = [56,1].](https://img.zadania.info/zad/6905815/HzadR2x.gif)
Wektory nie są równe, więc czworokąt 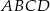 nie jest równoległobokiem.
nie jest równoległobokiem.
Sposób II
Wystarczy sprawdzić czy 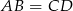 oraz
oraz 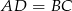 . Liczymy
. Liczymy
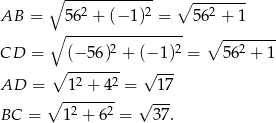
Ponieważ 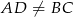 czworokąt
czworokąt 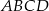 nie jest równoległobokiem.
nie jest równoległobokiem.
Sposób III
Czworokąt jest równoległobokiem wtedy i tylko wtedy, gdy jego przekątne dzielą się na połowy. Sprawdźmy, czy środki 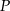 i
i 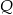 przekątnych
przekątnych 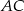 i
i 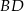 pokrywają się.
pokrywają się.
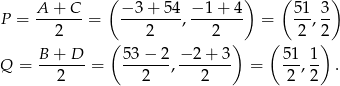
Skoro środki przekątnych to dwa różne punkty, to dany czworokąt nie jest równoległobokiem.
Odpowiedź: Nie, nie jest.

