/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 6965749

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt 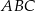ABC o wierzchołkach: 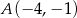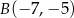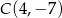A(− 4,− 1) , B(− 7,− 5) , C (4,− 7) . Oblicz długość odcinka 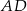AD dwusiecznej kąta przy wierzchołku A .

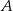Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

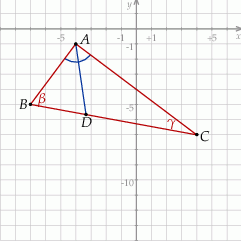
Jeżeli wykonamy dość dokładny rysunek, to możemy zauważyć, że trójkąt 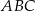ABC wydaje się być prostokątny. Aby sprawdzić, czy tak jest rzeczywiście, liczymy długości jego boków.

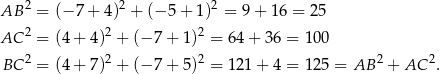
AB 2 = (− 7 + 4)2 + (− 5+ 1)2 = 9 + 16 = 2 5 2 2 2 AC = (4 + 4) + (− 7+ 1) = 64 + 36 = 100 BC 2 = (4 + 7)2 + (− 7+ 5)2 = 121 + 4 = 125 = AB 2 + AC 2.

Zatem rzeczywiście, trójkąt 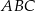ABC jest trójkątem prostokątnym z kątem prostym przy wierzchołku 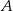A . W szczególności,

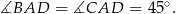
∡BAD = ∡CAD = 45∘ .

Długość dwusiecznej 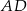AD obliczymy z twierdzenia sinusów, ale zanim to zrobimy, zauważmy, że

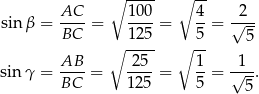
∘ ---- ∘ -- AC 100 4 2 sin β = ---- = ----= --= √--- BC ∘ -125 ∘ 5- 5 AB 25 1 1 sinγ = ---- = ----= --= √--. BC 125 5 5

Stosujemy teraz twierdzenie sinusów w trójkącie 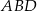ABD .

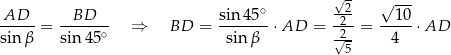
∘ √-2 √ --- AD--- = --BD--- ⇒ BD = sin-45- ⋅AD = -2- = --10-⋅AD sinβ sin 45∘ sin β √2- 4 5

Teraz stosujemy twierdzenie sinusów w trójkącie ACD .

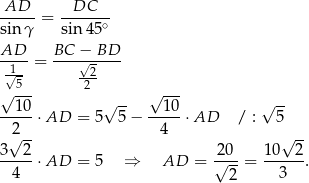
AD---= --DC--- sin γ sin 45∘ AD BC − BD -1--= ----√----- √-5 22- √ --- √ --- --10-⋅AD = 5√ 5-− --10-⋅AD / : √ 5- 2 4 3√ 2- 20 10√ 2- -----⋅AD = 5 ⇒ AD = √---= ------. 4 2 3

 
Odpowiedź: √ - 103-2

Wersja PDF