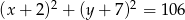Zadanie nr 7041460
Napisz równanie okręgu o środku 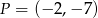 , którego punkty wspólne z okręgiem o równaniu
, którego punkty wspólne z okręgiem o równaniu 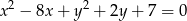 są końcami odcinka o długości
są końcami odcinka o długości 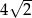 .
.
Rozwiązanie
Zapiszmy równanie danego okręgu tak, aby było widać jaki ma środek i promień.
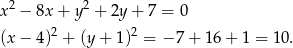
Jest to więc okrąg o środku 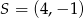 i promieniu
i promieniu 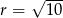 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
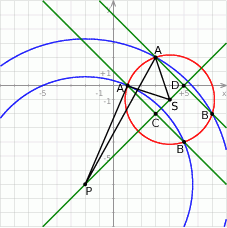
Sposób I
Z rysunku powinno być jasne, że będą dwa okręgi spełniające warunki zadania. Odległość między środkami okręgów jest równa
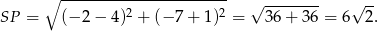
Zajmijmy się najpierw sytuacją, gdy wspólna cięciwa 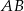 obu okręgów przecina odcinek
obu okręgów przecina odcinek 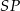 w punkcie
w punkcie 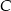 . Mamy wtedy
. Mamy wtedy
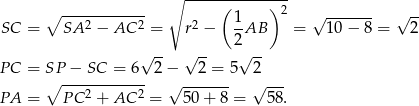
W tej sytuacji szukany okrąg ma więc równanie
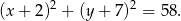
Zajmijmy się teraz drugą sytuacją, gdy punkt wspólny  cięciwy
cięciwy  i prostej
i prostej 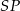 leży poza odcinkiem
leży poza odcinkiem 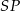 . Wtedy
. Wtedy
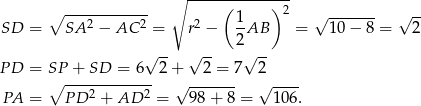
Drugi z szukanych okręgów ma więc równanie
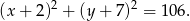
Sposób II
Szukamy okręgu postaci
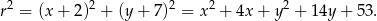
Punkty wspólne 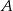 i
i 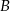 tego okręgu i okręgu danego w treści zadania są rozwiązaniami układu równań
tego okręgu i okręgu danego w treści zadania są rozwiązaniami układu równań
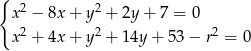
Odejmujemy od drugiego równania pierwsze i mamy
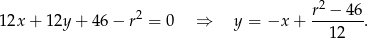
Żeby nie męczyć się z ułamkami oznaczmy 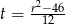 . Podstawiamy teraz
. Podstawiamy teraz 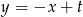 do pierwszego równania układu.
do pierwszego równania układu.
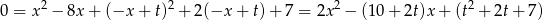
Jeżeli 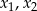 są rozwiązaniami powyższego równania, to
są rozwiązaniami powyższego równania, to 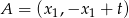 i
i 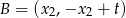 są punktami wspólnymi dwóch okręgów. Spróbujmy rozszyfrować informację o długości cięciwy
są punktami wspólnymi dwóch okręgów. Spróbujmy rozszyfrować informację o długości cięciwy 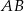 .
.
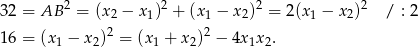
Na mocy wzorów Viète’a mamy więc równanie.
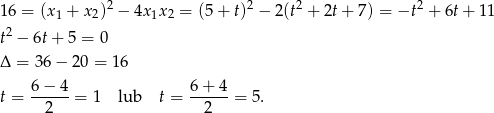
Stąd 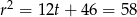 lub
lub 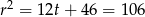 .
.
Odpowiedź: 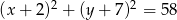 lub
lub