/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7072986

Dodaj do ulubionych
Dodaj do rozwiązanych

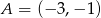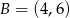W układzie współrzędnych dane są punkty A = (− 3,− 1) i B = (4,6 ) . Na wykresie funkcji 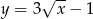√ -- y = 3 x − 1 znajdź taki punkt 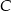C , dla którego pole trójkąta 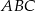ABC jest najmniejsze.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

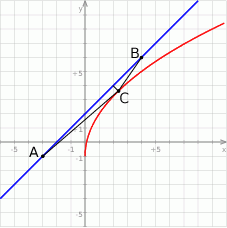
Sposób I

Zauważmy, że ponieważ podstawa 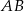AB trójkąta 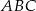ABC jest ustalona, jego pole zależy tylko i wyłącznie od długości wysokości opuszczonej z wierzchołka 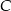C . Z kolei ta wysokość to odległość punktu 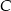C od prostej 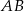AB . Musimy zatem znaleźć na danym wykresie punkt 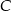C , dla którego odległość od prostej 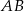AB jest najmniejsza.

Rozpoczynamy od napisania równania prostej 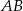AB . Podstawiamy do równania prostej postaci 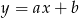y = ax + b współrzędne punktów 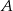A i B .

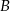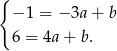
{ − 1 = − 3a + b 6 = 4a + b.

Odejmując od drugiego równania pierwsze mamy 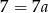7 = 7a , czyli 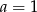a = 1 . Stąd 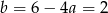b = 6− 4a = 2 i prosta 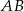AB ma równanie 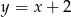y = x + 2 . Aby nie mieć pierwiastków zapiszmy dany wzór funkcji w postaci

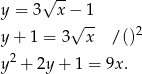
√ -- y = 3 x − 1 √ -- 2 y + 1 = 3 x / () y2 + 2y + 1 = 9x.

Oczywiście powyższe przekształcenie ma sens przy założeniu, że 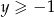y ≥ − 1 i x ≥ 0 .

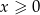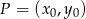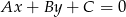Korzystając ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

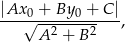
|Ax-0-+-By-0 +-C|- √ --2----2- , A + B

wiemy, że odległość punktu 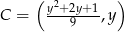( ) C = y2+-2y+-1,y 9 od prostej 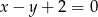x− y+ 2 = 0 jest równa

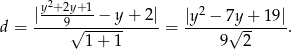
y2+ 2y+ 1 2 |---9---−--y+--2| |y--−-7y-+-19| d = √ 1+ 1 = 9√ 2 .

Zauważmy, że trójmian pod wartością bezwzględną jest zawsze dodatni (bo 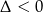Δ < 0 ), więc pozostało znaleźć najmniejszą wartość funkcji

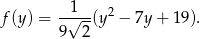
1 2 f (y) = -√---(y − 7y+ 19). 9 2

Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla 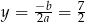y = −2ba-= 72 . Wtedy

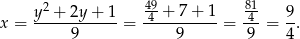
y2-+-2y-+-1- 494-+-7-+-1- 841- 9- x = 9 = 9 = 9 = 4.

Sposób II

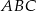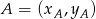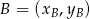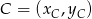Tym razem obliczamy pole trójkąta ABC korzystając ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

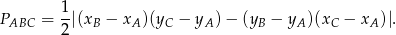
PABC = 1-|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|. 2

W naszej sytuacji 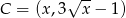√ -- C = (x,3 x − 1) i mamy

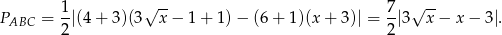
1 √ -- 7 √ -- PABC = -|(4 + 3)(3 x − 1 + 1) − (6 + 1)(x + 3 )| = -|3 x − x − 3|. 2 2

Aby pozbyć się pierwiastka podstawmy 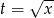√ -- t = x . Mamy wtedy oczywiście 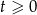t ≥ 0 oraz

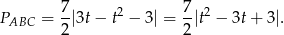
P = 7|3t− t2 − 3| = 7|t2 − 3t + 3|. ABC 2 2

Zauważmy teraz, że trójmian pod wartością bezwzględną jest zawsze dodatni (bo 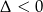Δ < 0 ), więc

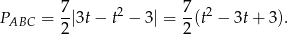
P = 7|3t− t2 − 3| = 7-(t2 − 3t + 3). ABC 2 2

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość pola otrzymamy w wierzchołku, czyli dla

3 t = 2.

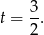
Mamy wtedy 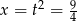x = t2 = 9 4 i

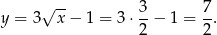
√ -- 3- 7- y = 3 x− 1 = 3 ⋅2 − 1 = 2.

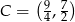Zatem ( ) C = 94, 72 .  
Odpowiedź: C = (9, 7) 4 2

Wersja PDF