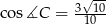Zadanie nr 7112795
Wyznacz kąty trójkąta  o wierzchołkach
o wierzchołkach 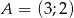 ,
, 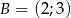 ,
, 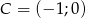 .
.
Rozwiązanie
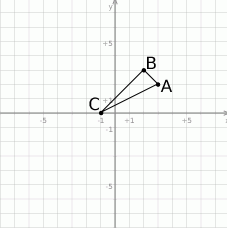
Na początek możemy sobie naszkicować podany trójkąt.
Kąty trójkąta wyliczymy posługując się iloczynem skalarnym wektorów, tzn. skorzystamy ze wzoru
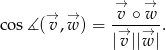
Jeżeli ktoś nie lubi wektorów, to równoważnie może użyć twierdzenia cosinusów. Aby policzyć cosinus kata 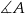 , wyznaczamy
, wyznaczamy ![→AB = [− 1,1]](https://img.zadania.info/zad/7112795/HzadR3x.gif) i
i ![→ AC = [−4 ,−2 ]](https://img.zadania.info/zad/7112795/HzadR4x.gif) . Mamy zatem
. Mamy zatem
![√ --- [−-1,1]∘-[−-4,−-2]- --4−--2--- ---10 co s∡A = √ 1-+-1-⋅√ 16+--4-= √ -- √ --= 10 . 2⋅ 2 5](https://img.zadania.info/zad/7112795/HzadR5x.gif)
Podobnie, ponieważ ![→ BA = [1,− 1]](https://img.zadania.info/zad/7112795/HzadR6x.gif) i
i ![→ BC = [− 3,− 3]](https://img.zadania.info/zad/7112795/HzadR7x.gif) , mamy
, mamy
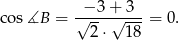
Czyli 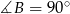 . W końcu,
. W końcu, ![→ CA = [4,2]](https://img.zadania.info/zad/7112795/HzadR10x.gif) ,
, ![→ CB = [3 ,3 ]](https://img.zadania.info/zad/7112795/HzadR11x.gif) , skąd
, skąd
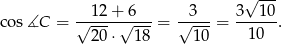
Odpowiedź: 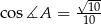 ,
, 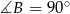 ,
,