Zadanie nr 7137969
Punkty 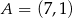 i
i 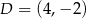 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 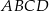 . Podstawa
. Podstawa 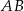 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 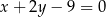 . Osią symetrii tego trapezu jest prosta o równaniu
. Osią symetrii tego trapezu jest prosta o równaniu 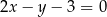 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 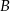 i
i 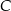 trapezu.
trapezu.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
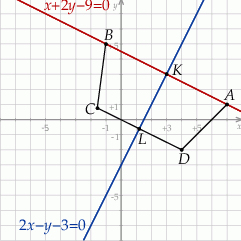
Wyznaczamy punkt 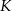 przecięcia się podanych dwóch prostych
przecięcia się podanych dwóch prostych
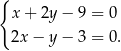
Dodajemy do pierwszego równania drugie pomnożone przez 2 (żeby zredukować 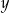 ) i mamy
) i mamy

Z drugiego równania 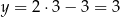 , czyli
, czyli 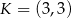 .
.
Punkt 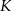 jest środkiem odcinka
jest środkiem odcinka 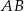 , więc korzystając ze wzoru na środek odcinka możemy wyznaczyć współrzędne punktu
, więc korzystając ze wzoru na środek odcinka możemy wyznaczyć współrzędne punktu 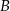 .
.
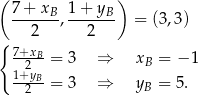
Zatem 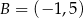 .
.
Dokładnie w ten sam sposób możemy wyznaczyć współrzędne punktu 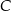 , ale najpierw musimy napisać równanie prostej
, ale najpierw musimy napisać równanie prostej 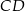 . Jest to prosta równoległa do
. Jest to prosta równoległa do 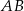 , więc ma równanie postaci
, więc ma równanie postaci 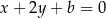 . Współczynnik
. Współczynnik 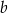 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 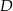 .
.
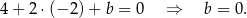
Zatem prosta 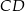 ma równanie
ma równanie 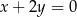 .
.
Wyznaczamy punkt 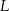 przecięcia się prostych
przecięcia się prostych 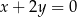 i
i 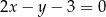
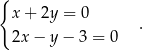
Dodajemy do pierwszego równania drugie pomnożone przez 2 (żeby skrócić 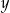 ) i mamy
) i mamy
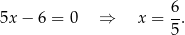
Z drugiego równania mamy
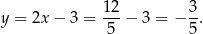
Zatem 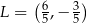 .
.
Podobnie jak wcześniej, ze wzoru na środek odcinka wyznaczamy współrzędne punktu 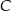
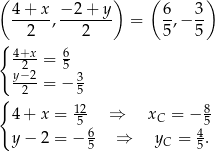
Zatem punkt 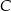 ma współrzędne
ma współrzędne
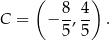
Odpowiedź: 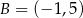 i
i