/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7142261

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że czworokąt o wierzchołkach 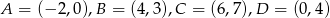A = (− 2,0),B = (4,3),C = (6,7),D = (0,4) jest trapezem.

Rozwiązanie

Musimy pokazać, że któraś para boków jest równoległa. Wyznaczmy równania prostych przechodzących przez kolejne pary punktów. Skorzystamy ze wzoru na prostą przechodzącą przez dwa punkty

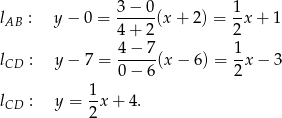
l : y − 0 = 3−--0(x + 2) = 1x + 1 AB 4+ 2 2 4− 7 1 lCD : y − 7 = -----(x − 6) = -x − 3 0− 6 2 l : y = 1x + 4. CD 2

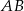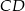Ponieważ współczynniki kierunkowe tych prostych są takie same, więc są one równoległe. Zatem boki AB i CD są równoległe, czyli czworokąt 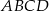ABCD jest trapezem. Jeszcze rysunek

PIC

Wersja PDF