Zadanie nr 7256790
Dane są dwa nieskończone ciągi 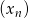 i
i 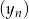 takie, że dla każdego
takie, że dla każdego 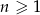 , punkt o współrzędnych
, punkt o współrzędnych 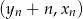 jest środkiem ciężkości trójkąta o wierzchołkach
jest środkiem ciężkości trójkąta o wierzchołkach 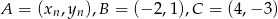 . Wyznacz wzory ciągów
. Wyznacz wzory ciągów 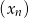 i
i 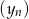 .
.
Rozwiązanie
Naszkicujmy trójkąt ze środkiem ciężkości.
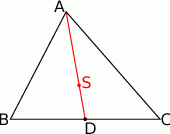
Sposób I
Środek ciężkości trójkąta to punkt przecięcia się jego środkowych i jak wiadomo dzieli on każdą ze środkowych w stosunku 2:1 licząc od wierzchołka. Jeżeli więc 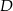 jest środkiem boku
jest środkiem boku 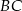 , czyli
, czyli
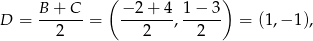
to
![−→ −→ AS = 2SD [yn + n − xn,xn − yn] = 2[1 − yn − n,− 1 − xn ] { yn + n − xn = 2− 2yn − 2n { xn − yn = −2 − 2xn 3y + 3n − 2 = x n n 3xn + 2 = yn](https://img.zadania.info/zad/7256790/HzadR4x.gif)
Podstawiamy 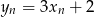 z drugiego równania do pierwszego i mamy
z drugiego równania do pierwszego i mamy
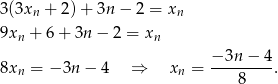
Zatem
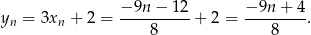
Sposób II
Zamiast wyliczać współrzędne środka ciężkości trójkąta mogliśmy skorzystać z gotowego wzoru
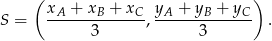
Otrzymujemy z niego
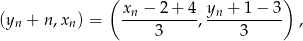
co prowadzi do układu równań
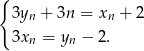
Układ ten rozwiązujemy tak samo jak w pierwszym sposobie.
Odpowiedź: 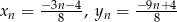 dla
dla 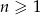 .
.

