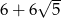/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7389505

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz obwód trójkąta o wierzchołkach: 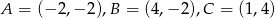A = (− 2,− 2),B = (4 ,− 2 ),C = (1,4) .

Rozwiązanie

Zaczynamy od narysowania trójkąta.

PIC

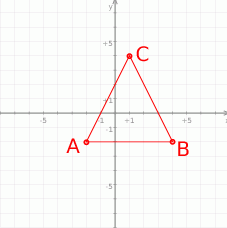
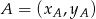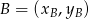Będziemy korzystać ze wzoru na odległość dwóch punktów A = (xA ,yA) i B = (xB,yB ) :

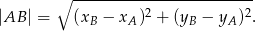
∘ ------------------------- |AB | = (x − x )2 + (y − y )2. B A B A

Ponieważ bok 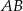AB jest równoległy do osi 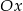Ox to ma długość 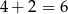4 + 2 = 6 . Policzmy długości pozostałych boków.

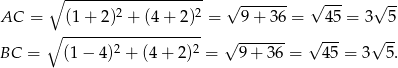
∘ ------------------- √ ------- √ --- √ -- AC = (1+ 2)2 + (4 + 2 )2 = 9+ 36 = 45 = 3 5 ∘ ------------------- √ ------- √ --- √ -- BC = (1 − 4)2 + (4 + 2)2 = 9 + 36 = 45 = 3 5 .

 
Odpowiedź: √ -- 6 + 6 5

Wersja PDF