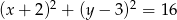/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7458316

Dodaj do ulubionych
Dodaj do rozwiązanych

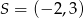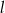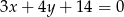Wyznacz równanie okręgu o środku S = (− 2,3) stycznego do prostej l o równaniu 3x + 4y + 14 = 0 .

Rozwiązanie

Ponieważ prosta 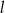l jest styczna do okręgu, więc odległość środka okręgu od prostej 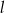l będzie równa promieniowi tego okręgu. Liczymy

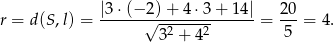
r = d(S ,l) = |3⋅(−-2√)-+-4-⋅3+--14| = 2-0 = 4. 32 + 42 5

Zatem okrąg ma równanie

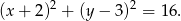
(x + 2)2 + (y − 3)2 = 16.

Na koniec obrazek

PIC

 
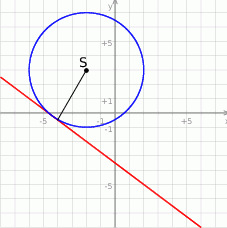
Odpowiedź: (x + 2)2 + (y − 3)2 = 16

Wersja PDF