/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7468452

Dodaj do ulubionych
Dodaj do rozwiązanych

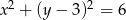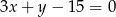Ile punktów wspólnych ma okrąg o równaniu 2 2 x + (y − 3) = 6 z prostą o równaniu 3x + y − 15 = 0 ?

Rozwiązanie

Sposób I

Z równania prostej wyznaczamy

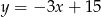
y = − 3x + 15

i podstawiamy do równania okręgu.

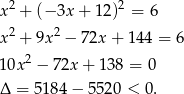
2 2 x + (− 3x + 1 2) = 6 x 2 + 9x 2 − 72x+ 144 = 6 10x 2 − 72x + 138 = 0 Δ = 518 4− 5 520 < 0.

Skoro równanie to nie ma rozwiązań, dane okrąg i prosta nie przecinają się.

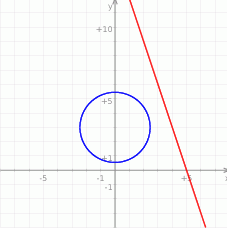
Na koniec obrazek.

PIC

Sposób II

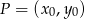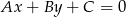Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

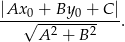
|Ax-0√-+-By-0 +-C|- A 2 + B 2 .

Liczymy odległość środka okręgu 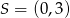S = (0,3) od danej prostej.

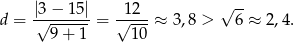
|3-−-15| -12-- √ -- d = √ 9+--1-= √ ---≈ 3 ,8 > 6 ≈ 2,4 . 10

To oznacza, że prosta nie przecina okręgu.  
Odpowiedź: 0

Wersja PDF