Zadanie nr 7490722
Proste 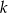 i
i 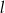 przecinają się w punkcie
przecinają się w punkcie 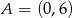 . Prosta
. Prosta 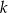 przecina ujemną półoś
przecina ujemną półoś 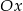 w punkcie
w punkcie 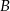 i tworzy z osiami układu trójkąt o polu 6, a prosta
i tworzy z osiami układu trójkąt o polu 6, a prosta 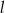 przecina dodatnią półoś
przecina dodatnią półoś 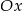 w punkcie
w punkcie 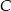 i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta
i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta 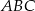 opuszczonej z wierzchołka
opuszczonej z wierzchołka 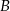 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
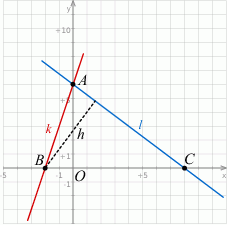
Trójkąty 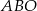 i
i 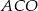 utworzone przez proste
utworzone przez proste 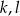 i osie układu są oba prostokątne i jedna z ich przyprostokątnych ma długość
i osie układu są oba prostokątne i jedna z ich przyprostokątnych ma długość 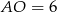 . Z podanych pól mamy
. Z podanych pól mamy
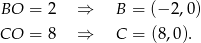
Sposób I
Pole trójkąta 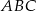 jest sumą pól trójkątów
jest sumą pól trójkątów 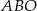 i
i 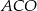 , wiec jest równe
, wiec jest równe 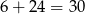 . Aby obliczyć długość wysokości
. Aby obliczyć długość wysokości 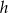 opuszczonej z wierzchołka
opuszczonej z wierzchołka 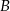 obliczamy długość odcinka
obliczamy długość odcinka 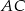 .
.
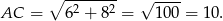
Korzystamy teraz ze wzoru na pole trójkąta.
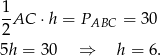
Sposób II
Zauważmy, że
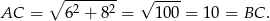
To oznacza, że trójkąt 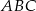 jest równoramienny. W szczególności jego wysokości opuszczone z wierzchołków
jest równoramienny. W szczególności jego wysokości opuszczone z wierzchołków 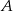 i
i 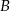 mają równe długości. Stąd
mają równe długości. Stąd
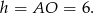
Odpowiedź: 6

