Zadanie nr 7523804
Dane są dwa wierzchołki 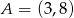 i
i 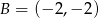 prostokąta
prostokąta 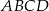 oraz punkt
oraz punkt 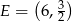 leżący na prostej
leżący na prostej 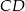 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 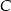 i
i 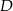 tego prostokąta.
tego prostokąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
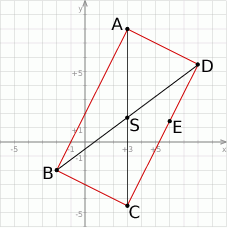
Napiszmy najpierw równanie prostej 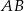 . Szukamy prostej w postaci
. Szukamy prostej w postaci 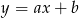 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 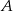 i
i 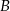 .
.
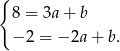
Odejmujemy od pierwszego równania drugie i mamy
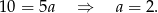
Współczynnika 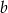 nie obliczamy, bo nie będzie nam potrzebny.
nie obliczamy, bo nie będzie nam potrzebny.
Możemy teraz napisać równanie prostej 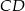 – jest równoległa do
– jest równoległa do 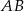 , więc ma równanie postaci
, więc ma równanie postaci 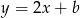 . Współczynnik
. Współczynnik 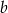 wyznaczmy podstawiając współrzędne punktu
wyznaczmy podstawiając współrzędne punktu 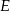 .
.
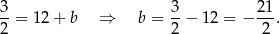
Prosta 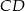 ma więc równanie
ma więc równanie 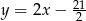 .
.
Piszemy teraz równanie prostej 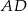 – jest ona prostopadła do
– jest ona prostopadła do 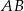 , więc ma równanie postaci
, więc ma równanie postaci 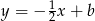 . Współczynnik
. Współczynnik 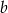 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 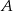 .
.
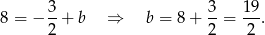
Prosta 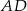 ma więc równanie
ma więc równanie 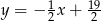 .
.
Szukamy teraz punktu wspólnego 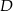 prostych
prostych 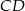 i
i 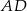
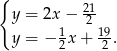
Odejmujemy od pierwszego równania drugie i mamy
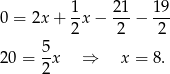
Stąd 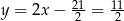 i
i 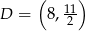 .
.
Współrzędne punktu 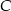 wyznaczymy na dwa sposoby.
wyznaczymy na dwa sposoby.
Sposób I
Liczymy dokładnie tak samo jak w przypadku punktu 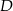 – szukamy równania prostej
– szukamy równania prostej 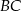 w postaci
w postaci 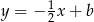 i podstawiamy w tym równaniu współrzędne punktu
i podstawiamy w tym równaniu współrzędne punktu 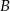 .
.
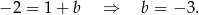
Prosta 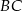 ma więc równanie
ma więc równanie 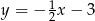 . Szukamy jej punktu wspólnego
. Szukamy jej punktu wspólnego 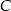 z prostą
z prostą 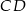 .
.
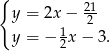
Odejmujemy od pierwszego równania drugie i mamy
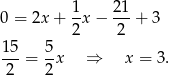
Stąd 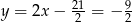 i
i 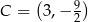 .
.
Sposób II
Wyznaczmy współrzędne środka prostokąta (czyli punktu przecięcia przekątnych) 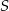 .
.
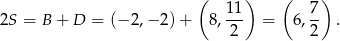
Z drugiej strony ten sam punkt jest środkiem odcinka 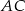 , więc
, więc
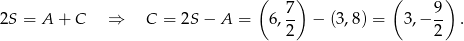
Odpowiedź: 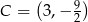 i
i