/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7618925

Dodaj do ulubionych
Dodaj do rozwiązanych

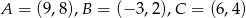Punkty A = (9,8),B = (− 3,2),C = (6,4) są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 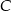C przecina prostą 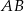AB w punkcie 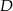D . Oblicz współrzędne punktu D .

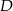Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

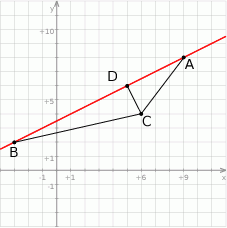
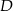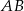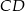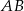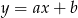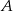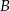Aby wyznaczyć współrzędne punktu D potrzebujemy znać równania prostych AB i CD . Zacznijmy od AB . Szukamy prostej postaci y = ax + b . Podstawiając współrzędne punktów A i B mamy układ równań

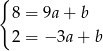
{ 8 = 9a + b 2 = − 3a + b

Odejmując od pierwszego równania drugie mamy

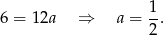
6 = 12a ⇒ a = 1-. 2

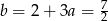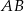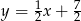Zatem b = 2 + 3a = 72 i prosta AB ma równanie y = 12x + 72 .

Prosta 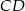CD jest prostopadła do 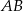AB , czyli ma postać 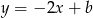y = − 2x + b i przechodzi przez punkt 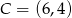C = (6,4) skąd

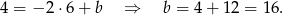
4 = − 2⋅ 6+ b ⇒ b = 4 + 12 = 1 6.

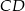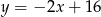Zatem prosta CD ma równanie y = − 2x + 1 6 .

Szukamy teraz punktu wspólnego 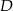D prostych 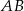AB i CD .

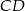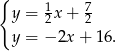
{ y = 1x + 7 2 2 y = − 2x + 16.

Odejmując od pierwszego równania drugie mamy

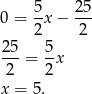
5 25 0 = 2-x− 2-- 25 5 ---= -x 2 2 x = 5.

Stąd 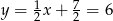y = 1 x+ 7 = 6 2 2 i D = (5,6 ) .  
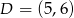Odpowiedź: D = (5,6)

Wersja PDF